题目内容
【题目】一长直杆长1.5 m , 垂直立于底部平坦、水面平静无波的游泳池中,露出水面部分高0.3 m , 当阳光以与水面成37°的夹角入射时,杆在游泳池底部所成的影长为多少?(已知水的折射率n=![]() .)
.)
【答案】依题意作图如图所示,依据折射定律n=![]() ,得sin θ2=
,得sin θ2=![]() =
=![]() =
=![]() ,∠θ2=37°,影长s=0.3×tan 53° m+1.2×tan 37° m=0.3× m+1.2× m=1.3 m .
,∠θ2=37°,影长s=0.3×tan 53° m+1.2×tan 37° m=0.3× m+1.2× m=1.3 m . 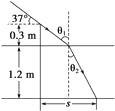
【解析】利用光路图解决光的折射问题的方法:(1)根据题意画出正确的光路图.首先要找到入射的界面,同时准确地作出法线,再根据折射定律和入射光线画出折射光线,找到入射角和折射角,要注意入射角、折射角是入射光线、折射光线与法线的夹角.(2)利用几何关系确定光路图中的边、角关系,与折射定律n=中的各量准确对应,比如一定要确定准哪个角在分子上、哪个角在分母上.(3)利用折射定律n=、折射率与光速的关系n=列方程,结合数学三角函数的关系进行运算.
【考点精析】解答此题的关键在于理解光的折射的相关知识,掌握光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射.

练习册系列答案
相关题目