题目内容
如图2-16(原图2-24)所示,两等高光滑的斜面AC和A'B'C'固定.已知斜面总长AC = A′B′+B′C′,且θ>θ′.让小球分别从两斜面顶端无初速滑下,到达斜面底部的时间分别为t和t′.若则t和t′应当是什么关系?[8]


t>t′
如图2-17所示,在AC段取一点B,使AB = A′B′,由θ>θ′可知,小球到达B点的速度小于小球到达B′点的速度,即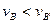 ,
,
又因为两斜面等高、光滑、不计在转折处的碰撞损失,由下落过程中机械能守恒知,在C点和C′点速率相等,即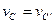 ,
,
小球从A到C的时间为:
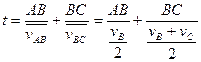 , ①
, ①
小球从A′到C′的时间为:
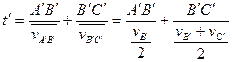 , ②
, ②
由于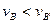 ,
,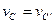 ,AB = A′B′, BC = B′C′,比较①、②两式可得:
,AB = A′B′, BC = B′C′,比较①、②两式可得:
t>t′,
故t和t′的关系应当是t>t′。
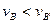 ,
,又因为两斜面等高、光滑、不计在转折处的碰撞损失,由下落过程中机械能守恒知,在C点和C′点速率相等,即
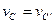 ,
,小球从A到C的时间为:
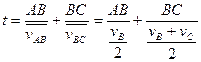 , ①
, ①小球从A′到C′的时间为:
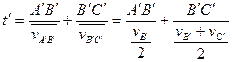 , ②
, ②由于
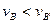 ,
,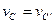 ,AB = A′B′, BC = B′C′,比较①、②两式可得:
,AB = A′B′, BC = B′C′,比较①、②两式可得:t>t′,
故t和t′的关系应当是t>t′。

练习册系列答案
相关题目

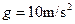 )以醒世人。意思是如果行车加速度达到此值,将有生命危险。这么大的加速度,一般车辆是达不到的,但是如果发生交通事故时,将会达到这一数值。
)以醒世人。意思是如果行车加速度达到此值,将有生命危险。这么大的加速度,一般车辆是达不到的,但是如果发生交通事故时,将会达到这一数值。 s,你判定一下驾驶员是否有生命危险?
s,你判定一下驾驶员是否有生命危险?
