题目内容
(14分)如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为 ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成 角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标。
 ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成 角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标。

(1)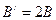
(2)x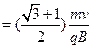
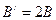
(2)x
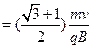
(1)设质子在磁场I和II中做圆周运动的轨道半径分别为 和
和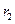 ,区域II中磁感应强度为
,区域II中磁感应强度为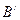 ,由牛顿第二定律
,由牛顿第二定律
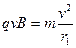 ①(2分)
①(2分)
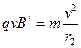 ②(2分)
②(2分)
粒子在两区域运动的轨迹如图所示,
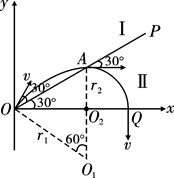
由几何关系可知,质子从A点出磁场I时的
速度方向与OP的夹角为300,故质子在磁场I中轨迹的圆心角为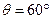
则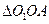 为等边三角形
为等边三角形  ③(2分)
③(2分)
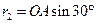 ④(2分)
④(2分)
由①②③④解得区域II中磁感应强度为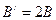 (2分)
(2分)
(2)Q点坐标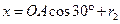 (2分) 故 x
(2分) 故 x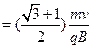 (2分)
(2分)
 和
和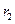 ,区域II中磁感应强度为
,区域II中磁感应强度为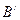 ,由牛顿第二定律
,由牛顿第二定律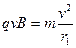 ①(2分)
①(2分)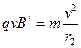 ②(2分)
②(2分)粒子在两区域运动的轨迹如图所示,

由几何关系可知,质子从A点出磁场I时的
速度方向与OP的夹角为300,故质子在磁场I中轨迹的圆心角为
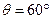
则
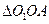 为等边三角形
为等边三角形  ③(2分)
③(2分)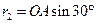 ④(2分)
④(2分)由①②③④解得区域II中磁感应强度为
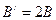 (2分)
(2分)(2)Q点坐标
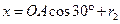 (2分) 故 x
(2分) 故 x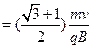 (2分)
(2分)
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 直纸面向里的匀强磁场,则磁场的磁感应强度不能超过多少(用m、v、q、R表示)?若满足此条件,从O点发射出的所有带电粒子中有几分之几能打在板的左边?
直纸面向里的匀强磁场,则磁场的磁感应强度不能超过多少(用m、v、q、R表示)?若满足此条件,从O点发射出的所有带电粒子中有几分之几能打在板的左边?
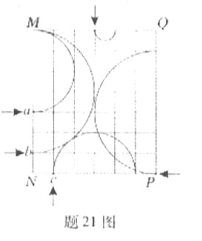

 m。已知粒子
m。已知粒子 能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求:
能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求:


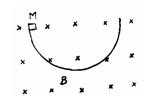
 :1
:1