题目内容
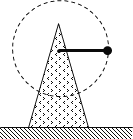
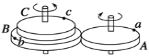
【题目】如图所示装置可绕竖直轴OO′转动,可视为质点的小球A与两细线连接后分别系于B、C两点,当细线AB沿水平方向绷直时,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长L=1m。(重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8)
(1)若装置匀速转动,细线AB刚好被拉直成水平状态,求此时的角速度ω1的大小;
(2)若装置匀速转动的角速度ω2=![]() rad/s,求细线AB和AC上的张力大小TAB、TAC。
rad/s,求细线AB和AC上的张力大小TAB、TAC。

【答案】(1)![]() rad/s;(2)2.5N,12.5N
rad/s;(2)2.5N,12.5N
【解析】
(1)细线AB上张力恰为零时,小球靠重力和拉力的合力提供向心力,根据牛顿第二定律有
![]()
解得
![]()
(2)当![]() 时,
时,![]() ,线AB有张力,由小球的受力情况及牛顿第二定律得
,线AB有张力,由小球的受力情况及牛顿第二定律得
![]()
![]()
解得
![]()
![]()

练习册系列答案
相关题目