题目内容
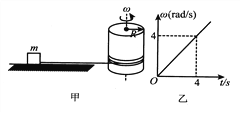
【题目】如图所示,质量m=2kg的小物体放在长直的水平地面上,用水平细线绕在半径R=0.5m的薄圆筒上。t=0时刻,圆筒由静止开始绕竖直的中心轴转动,其角速度随时间的变化规律如图乙所示,小物体和地面间的动摩擦因数![]() ,重力加速度g取10m/s2,则:
,重力加速度g取10m/s2,则:
A. 小物体的速度随时间的变化关系满足v=4t
B. 细线的拉力大小为2N
C. 细线拉力的瞬时功率满足P=4t
D. 在0~4s内,细线拉力做的功为12J
【答案】D
【解析】根据图象可知,圆筒做匀加速转动,角速度随时间变化的关系式为:ω=t,圆筒边缘线速度与物块前进速度大小相同,根据v=ωR得:v=ωR=0.5t,故A错误;物体运动的加速度![]() ,根据牛顿第二定律得:F-μmg=ma
,根据牛顿第二定律得:F-μmg=ma
解得:F=2×0.5+0.1×2×10=3N,故B错误;细线拉力的瞬时功P=Fv=3×0.5t=1.5t,故C错误;物体在4s内运动的位移:x=![]() at2=
at2=![]() ×0.5×42=4m,在0~4s内,细线拉力做的功为:W=Fx=3×4=12J,故D正确.故选D.
×0.5×42=4m,在0~4s内,细线拉力做的功为:W=Fx=3×4=12J,故D正确.故选D.

练习册系列答案
相关题目