题目内容
如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端向上弯曲,其余水平,水平导轨左端有宽度为d、方向竖直向上的匀强磁场I,右端有另一磁场II,其宽度也为d,但方向竖直向下,磁场的磁感强度大小均为B.有两根质量均为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场II中点C、D处,导轨除C、D两处(对应的距离极短)外其余均光滑,两处对棒可产生总的最大静摩擦力为棒重力的K倍,a棒从弯曲导轨某处由静止释放.当只有一根棒作切割磁感线运动时,它速度的减小量与它在磁场中通过的距离成正比,即△v∝△x.
(1)若a棒释放的高度大于h0,则a棒进入磁场I时会使b棒运动,判断b 棒的运动方向并求出h0.
(2)若将a棒从高度小于h0的某处释放,使其以速度v0进入磁场I,结果a棒以
的速度从磁场I中穿出,求在a棒穿过磁场I过程中通过b棒的电量q和两棒即将相碰时b棒上的电功率Pb.
(3)若将a棒从高度大于h0的某处释放,使其以速度v1进入磁场I,经过时间t1后a棒从磁场I穿出时的速度大小为
,求此时b棒的速度大小,在如图坐标中大致画出t1时间内两棒的速度大小随时间的变化图象,并求出此时b棒的位置.
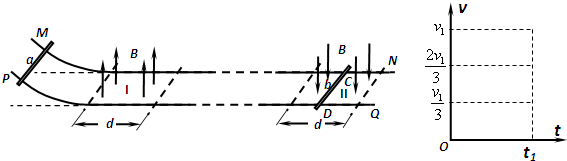
(1)若a棒释放的高度大于h0,则a棒进入磁场I时会使b棒运动,判断b 棒的运动方向并求出h0.
(2)若将a棒从高度小于h0的某处释放,使其以速度v0进入磁场I,结果a棒以
| v0 |
| 2 |
(3)若将a棒从高度大于h0的某处释放,使其以速度v1进入磁场I,经过时间t1后a棒从磁场I穿出时的速度大小为
| 2v1 |
| 3 |

分析:(1)a棒从h0高处释放后在弯曲导轨上滑动时机械能守恒求得速度,根据法拉第电磁感应定律求得电动势,在求出安培力.
(2)流过电阻R的电量q=
△t,求出电流,求出电功率.
(3)由于a棒从高度大于h0处释放,因此当a棒进入磁场I后,b棒开始向左运动.由于每时每刻流过两棒的电流强度大小相等,两磁场的磁感强度大小也相等,所以两棒在各自磁场中都做变加速运动,且每时每刻两棒的加速度大小均相同.
(2)流过电阻R的电量q=
. |
| I |
(3)由于a棒从高度大于h0处释放,因此当a棒进入磁场I后,b棒开始向左运动.由于每时每刻流过两棒的电流强度大小相等,两磁场的磁感强度大小也相等,所以两棒在各自磁场中都做变加速运动,且每时每刻两棒的加速度大小均相同.
解答:解:(1)根据左手定则判断知b棒向左运动.
a棒从h0高处释放后在弯曲导轨上滑动时机械能守恒,有
mgh0=
mv2
得v=
a棒刚进入磁场I时E=BLv
此时感应电流大小I=
此时b棒受到的安培力大小F=BIL
依题意,有F=Kmg
求得h0=
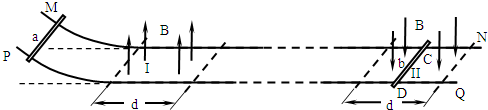
(2)由于a棒从小于进入h0释放,因此b棒在两棒相碰前将保持静止.
流过电阻R的电量q=
△t
又
=
=
所以在a棒穿过磁场I的过程中,通过电阻R的电量
q=
将要相碰时a棒的速度
v=
-
×
=
此时电流I=
此时b棒电功率Pb=I2R=
.
(3)由于a棒从高度大于h0处释放,因此当a棒进入磁场I后,b棒开始向左运动.由于每时每刻流过两棒的电流强度大小相等,两磁场的磁感强度大小也相等,所以两棒在各自磁场中都做变加速运动,且每时每刻两棒的加速度大小均相同,所以当a棒在t1时间内速度改变(v1-
v1)=
v1时,b棒速度大小也相应改变了
v1,即此时b棒速度大小为
v1.
两棒的速度大小随时间的变化图象大致如图所示:
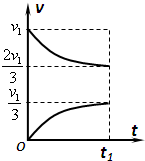
通过图象分析可知,在t1时间内,两棒运动距离之和为v1t1,所以在t1时间内b棒向左运动的距离为△S=(v1t1-d),
距离磁场II左边界距离为
△L=
-△S=
-v1t1.
a棒从h0高处释放后在弯曲导轨上滑动时机械能守恒,有
mgh0=
| 1 |
| 2 |
得v=
| 2gh0 |
a棒刚进入磁场I时E=BLv
此时感应电流大小I=
| E |
| 2R |
此时b棒受到的安培力大小F=BIL
依题意,有F=Kmg
求得h0=
| 2K2m2gR2 |
| B4L4 |

(2)由于a棒从小于进入h0释放,因此b棒在两棒相碰前将保持静止.
流过电阻R的电量q=
. |
| I |
又
. |
| I |
| ||
| R总 |
| B△S |
| R总△t |
所以在a棒穿过磁场I的过程中,通过电阻R的电量
q=
| BLd |
| 2R |
将要相碰时a棒的速度
v=
| v0 |
| 2 |
v0-
| ||
| d |
| d |
| 2 |
| v0 |
| 4 |
此时电流I=
| BLv0 |
| 8R |
此时b棒电功率Pb=I2R=
| ||
| 64R |
(3)由于a棒从高度大于h0处释放,因此当a棒进入磁场I后,b棒开始向左运动.由于每时每刻流过两棒的电流强度大小相等,两磁场的磁感强度大小也相等,所以两棒在各自磁场中都做变加速运动,且每时每刻两棒的加速度大小均相同,所以当a棒在t1时间内速度改变(v1-
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
两棒的速度大小随时间的变化图象大致如图所示:

通过图象分析可知,在t1时间内,两棒运动距离之和为v1t1,所以在t1时间内b棒向左运动的距离为△S=(v1t1-d),
距离磁场II左边界距离为
△L=
| d |
| 2 |
| 3d |
| 2 |
点评:本题考查了电磁感应中力学与功能问题,物理过程比较复杂,对于这类问题,理清解题的思路很重要.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( ) 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )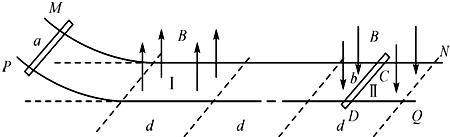
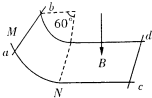 如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:
如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求: