题目内容
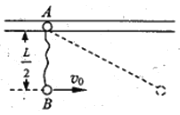
【题目】如图所示，质量为m、电荷量为q的带正电粒子，以速度v0从A点沿AB边射入边长为a的等边三角形的匀强磁场区域中，磁场方向垂直纸面向里，大小为B，不考虑粒子的重力，则（ ）
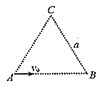
A. 若v0＝
，则粒子从A、C之间某点离开磁场
B. 若v0＝，则粒子刚好从C点离开磁场
C. 若v0＝
，则粒子从B、C边中点离开磁场
D. 若＜v0＜，则粒子从B、C之间某点射出磁场
【答案】B
【解析】
粒子在磁场中做匀速圆周运动，作出粒子运动轨迹，求出粒子临界轨道半径，然后应用牛顿第二定律求出粒子临界速度，再分析答题。
粒子恰好从C点离开磁场时运动轨迹如图所示：
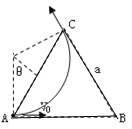
由几何知识得：θ＝60°，粒子轨道半径：r＝
，粒子在磁场中做匀速圆周运动，由牛顿第二定律得：qvB＝m
，解得：v＝
，粒子速度越小，粒子轨道半径越小，当v0＝时粒子从C点离开磁场，v0＜时粒子从AC边射出磁场，当v0＞时粒子从BC边射出磁场，故B正确，ACD错误；故选B。
练习册系列答案
相关题目
