��Ŀ����
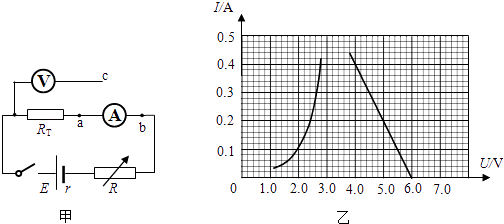
����Ŀ����ͼa��ʾ����˿K���������ݳ����Ƴ��ٶȵĵ��ӣ���KA�侭��СΪU�ļ��ٵ�ѹ���ٺ�A������С��������ٴ�M��N����������м���ƽ�м���ķ������ƫת�糡��M��N�����峤ΪL�����Ϊ ![]() L���������������ͼb��ʾ�ĵ�ѹUMN �� ����ǡ��ȫ��������ͼ��ʾ����ǿ�ų��У������Ǽ����Ե��Ӱ�죬���Ӵ���ƽ�а��ʱ�伫�ˣ���Խ���̿���Ϊ����ѹ���䣬�ų��� �뿪�ų������ʱ���Ƕ��٣�ֱֽ�������ҷ�Χ�㹻�����ǵ糡�仯�Դų���Ӱ�죮��֪���ӵ�����Ϊm�������Ϊe�����Ƶ��ӵ�����������֮��������������
L���������������ͼb��ʾ�ĵ�ѹUMN �� ����ǡ��ȫ��������ͼ��ʾ����ǿ�ų��У������Ǽ����Ե��Ӱ�죬���Ӵ���ƽ�а��ʱ�伫�ˣ���Խ���̿���Ϊ����ѹ���䣬�ų��� �뿪�ų������ʱ���Ƕ��٣�ֱֽ�������ҷ�Χ�㹻�����ǵ糡�仯�Դų���Ӱ�죮��֪���ӵ�����Ϊm�������Ϊe�����Ƶ��ӵ�����������֮��������������
��1��ƫת�糡��ѹUMN�ķ�ֵ��
��2����֪t= ![]() ��ʱ������ƫת�糡�ĵ���ǡ���ܷ��ذ�䣬����ǿ�ų��Ÿ�Ӧǿ��B�Ĵ�С��
��ʱ������ƫת�糡�ĵ���ǡ���ܷ��ذ�䣬����ǿ�ų��Ÿ�Ӧǿ��B�Ĵ�С��
��3���ӵ��ӽ���ƫת�糡��ʼ���뿪�ų������ʱ���Ƕ��٣�
���𰸡�
��1���⣺�����ھ������ٵ糡�����У����ݶ��ܶ����ɵã�eU= ![]()
�����⣬��ƫת��ѹ���ַ�ֵʱ����ĵ���ǡ���ؼ����Ե�ɳ��糡��
![]() =
= ![]()
a= ![]()
L=v0t
���������ϼ�ʽ�ɵã�Um= ![]()
��ƫת�糡��ѹUMN�ķ�ֵΪ ![]() ��
��
��2������t= ![]() ʱ�̽���ƫת�糡�ĵ����뿪�糡ʱ�ٶȴ�СΪv��v��v0֮��ļн�Ϊ�ȣ�
ʱ�̽���ƫת�糡�ĵ����뿪�糡ʱ�ٶȴ�СΪv��v��v0֮��ļн�Ϊ�ȣ�
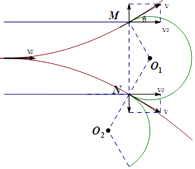
tan��= ![]() =
= ![]() =
= ![]()
v0=vcos��
���Ӵ�ֱ����ų������������䵱������ evB= ![]()
���ݼ��ι�ϵ 2Rcos��= ![]()
��ã�B= ![]()
����֪t= ![]() ��ʱ������ƫת�糡�ĵ���ǡ���ܷ��ذ�䣬���ʱ��ǿ�ų���ǿ��B�Ĵ�СΪ
��ʱ������ƫת�糡�ĵ���ǡ���ܷ��ذ�䣬���ʱ��ǿ�ų���ǿ��B�Ĵ�СΪ ![]() ��
��
��3��������ƫת�糡���˶���ʱ��ȣ�������ڴų���Բ���˶�����ΪT����N���Ե�ɳ��ĵ����ڴų����˶�ʱ����̣��ڴų��з���ʱ��Ϊ ![]()
T= ![]()
����������ʽ�ɵã�
tmin= ![]()
�𣺴ӵ��ӽ���ƫת�糡��ʼ���뿪�ų������ʱ���� ![]() ��
��
����������1�������⣬��������ǡ��ȫ���ӵ糡������ų�������ѹ���ַ�ֵʱ������ǡ�ôӼ����Ե��������ݴ��������ڵ糡������ƽ���˶����ɣ��������������ѹ�ķ�ֵ��
��2���ɼ��ι�ϵ���������t=![]() ʱ�̽���ƫת�糡�ĵ����ڴų���������Բ���˶��İ뾶�����ڵ���ǡ�ܷ��ؼ��壬�Ӷ��õ��ٶȺͽǶȹ�ϵ���Ӷ������������ṩ����������Ҳ�ų��ĴŸ�Ӧǿ�ȴ�С��
ʱ�̽���ƫת�糡�ĵ����ڴų���������Բ���˶��İ뾶�����ڵ���ǡ�ܷ��ؼ��壬�Ӷ��õ��ٶȺͽǶȹ�ϵ���Ӷ������������ṩ����������Ҳ�ų��ĴŸ�Ӧǿ�ȴ�С��
��3����Ȼ���Ӿ�N���Ե�ɳ��ĵ����ڴų����˶�ʱ����̣�ʱ��Ϊ![]() ���������ڵ糡�е�ʱ����ȣ����Ե��Ӵӽ���糡���뿪�ų������ʱ����������
���������ڵ糡�е�ʱ����ȣ����Ե��Ӵӽ���糡���뿪�ų������ʱ����������