题目内容
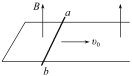
【题目】如图所示,足够长的木板与水平地面间的夹角θ可以调节,当木板与水平地面间的夹角为37°时,一小物块(可视为质点)恰好能沿着木板匀速下滑。若让该物块以大小v0=10m/s的初速度从木板的底端沿木板上滑,随着θ的改变,物块沿木板滑行的距离x将发生变化。取g=10m/s2,sin37°=0.6,cos37°=0.8。
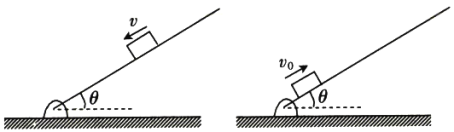
(1)求物块与木板间的动摩擦因数μ;
(2)当θ满足什么条件时,物块沿木板向上滑行的距离最小,并求出该最小距离。
【答案】(1) 0.75(2) 4m
【解析】
(1)当θ=37°时,设物块的质量为m,物块所受木板的支持力大小为FN,对物块受力分析,有:mgsin37°=μFN
FN-mgcos37°=0
解得:μ=0.75
(2)设物块的加速度大小为a,则有:mgsinθ+μmgcosθ=ma
设物块的位移为x,则有:v02=2ax
解得:![]()
令tanα=μ,可知当α+θ=90°,即θ=53°时x最小
最小距离为:xmin=4m

练习册系列答案
相关题目