��Ŀ����
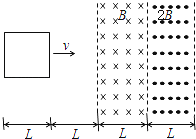
����Ŀ����ͼ��ʾ�������㹻���⻬ƽ�н�������PQ��MN��б�̶������Ϊ��=30�㣬���ΪL �� ���촦�ڴŸ�Ӧǿ��ΪB������ֱ����ƽ�����µ���ǿ�ų��У�������������Ϊm�Ľ�����a��b �� �Ƚ�a����ֱ������ã��ÿ���⻬�����ֵ�ϸ����С��c���ӣ�����a����ϸ��ƽ���ڵ��죬�ɾ�ֹ�ͷ�c �� �˺�ijʱ�̣���b��Ҳ��ֱ��������ڵ����ϣ�b�պ��ܾ�ֹ��a�����˶�������ʼ���뵼�촹ֱ�������뵼��Ӵ����ã�������費�ƣ��������ٶ�Ϊg �� ������ 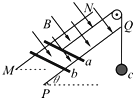
A.С��c������Ϊ2m
B.b�����ϵ���ǰa���ļ��ٶ�Ϊ0.5g
C.b�����ϵ����a���е�����С�� ![]()
D.b�����ϵ����С��c���ٵ��������ܵ��ڻ�·���ĵĵ���
���𰸡�C
�����������A��b����ֹ��˵��b������ƽ�⣬����������������б�����µķ���ƽ�⣬a�����������˶���˵��a��������������������б�����µķ�����С�Լ���б�����µİ�����������ƽ�⣬c�����½���c��������������������Сƽ�⣮��b �� ��ƽ��������֪����������С F��=mgsin�� �� ��a �� ��ƽ��������֪ F��=F��+mgsin��=2mgsin�� �� ��cƽ���֪F��=mcg �� ��Ϊ����������С��ȣ���2mgsin��=mcg �� �����c������Ϊ mc=2msin��=m �� ��A��ȷ��
B��b����֮ǰ������ţ�ٵڶ����ɵã�b�ļ��ٶ� ![]() ����B����
����B����
C������b����ƽ���֪F��=mgsin��
����ΪF��=BIL �� �ɵ� ![]() ����C��ȷ��
����C��ȷ��
D��b�����ϵ����a����������a�������������ӣ��������غ�֪С��c���ٵ��������ܵ��ڻ�·���ĵĵ�����a���ӵ���������֮�ͣ���D����
��ѡ��C��
������a��b���и�Ӧ������С��ȷ����෴����a��b�����ܰ�������С��ȷ����෴����b���������������а�������С��������б�����µķ�����С��ȣ�����a��Ϊ�о���������a����ƽ�⼰�������Ĵ�С�����Կ�����������������پ�Cƽ����Եõ�C��������c���ٵ��������ܵ��ڸ������ӵ��������ܺͶ����Լ������ĵ��ܣ��ɴ˷�����֪��
�����㾫�����������⣬������Ҫ�˽���ζ���(��ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж����)��