题目内容
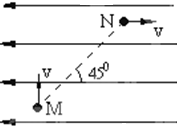 如图所示,有一带电微粒以5×105m/s的速度竖直向上从M点射入水平向左的匀强电场中,微粒的质量为10-6kg,电量为-2×10-8C,当它运动到比M点高出2cm的N点时,速度方向变为水平向右,大小等于初速度,MN连线与电场夹的最小角为45°,则电场强度为
如图所示,有一带电微粒以5×105m/s的速度竖直向上从M点射入水平向左的匀强电场中,微粒的质量为10-6kg,电量为-2×10-8C,当它运动到比M点高出2cm的N点时,速度方向变为水平向右,大小等于初速度,MN连线与电场夹的最小角为45°,则电场强度为分析:由动能定理求出电场强度的大小,然后由U=Ed求出电势差的大小.
解答:解:(1)由题意知:上升高度等于水平位移的大小,所以
由动能定理得:
Eqh-mgh=
mv2-
mv2
求解得:E=500V/m
(2)MN间的电势差U=Ed=Eh=500×0.02V=10V
故答案为:500V/m;10V
由动能定理得:
Eqh-mgh=
| 1 |
| 2 |
| 1 |
| 2 |
求解得:E=500V/m
(2)MN间的电势差U=Ed=Eh=500×0.02V=10V
故答案为:500V/m;10V
点评:此题考查带电粒子在电场中受力情况的分析,考查动能定理及电势差的公式的应用.

练习册系列答案
相关题目
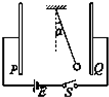 如图所示,P、Q为一平行板电容器的两个竖直放置的金属板,在两板间用绝缘线悬挂一带电小球,闭合开关S,小球静止时,悬线偏离竖直方向α角,则有( )
如图所示,P、Q为一平行板电容器的两个竖直放置的金属板,在两板间用绝缘线悬挂一带电小球,闭合开关S,小球静止时,悬线偏离竖直方向α角,则有( )| A、小球一定带正电 | B、若断开开关S,小球将回到竖直位置 | C、若断开开关S,将P板向上微移,悬线偏角将变大 | D、保持开关S闭合,将P板向左微移,悬线拉力将变小 |
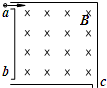 如图所示的正方形盒子开有a、b、c三个微孔,盒内有垂直纸面向里的匀强磁场.一束速率不同的带电粒子(质量、电量均相同,不计重力)从a孔沿垂直磁感线方向射入盒中,发现从c孔和b孔有粒子射出,试分析下列问题:
如图所示的正方形盒子开有a、b、c三个微孔,盒内有垂直纸面向里的匀强磁场.一束速率不同的带电粒子(质量、电量均相同,不计重力)从a孔沿垂直磁感线方向射入盒中,发现从c孔和b孔有粒子射出,试分析下列问题: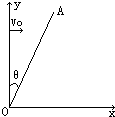 如图所示,直线OA与y轴成θ=30°角,在AOy范围内有沿y轴负方向的匀强电场,在AOx范围内有一个矩形区域的匀强磁场.该磁场区域的磁感应强度B=0.2T,方向垂直纸面向里.一带电微粒电荷量q=+2×10-14C,质量m=4×10-20kg,微粒子在y轴上的某点以速度v0垂直于y轴进入匀强电场,并以速度v=3×104m/s垂直穿过直线OA,运动中经过矩形磁场区域后,最终又垂直穿过x轴.不计微粒重力,求:(根据创新设计习题改编)
如图所示,直线OA与y轴成θ=30°角,在AOy范围内有沿y轴负方向的匀强电场,在AOx范围内有一个矩形区域的匀强磁场.该磁场区域的磁感应强度B=0.2T,方向垂直纸面向里.一带电微粒电荷量q=+2×10-14C,质量m=4×10-20kg,微粒子在y轴上的某点以速度v0垂直于y轴进入匀强电场,并以速度v=3×104m/s垂直穿过直线OA,运动中经过矩形磁场区域后,最终又垂直穿过x轴.不计微粒重力,求:(根据创新设计习题改编)
