题目内容
3.一辆值勤的警车停在公路边,当警员发现从他旁边以v=8m/s的速度匀速行驶的货车有违章行为时,决定去拦截.经2.5s警车发动起来,并以a=2m/s2加速度从静止匀加速追击货车,警车能达到的最大速度为v′=120Km/h.求:(1)警车从起动后要多长时间才能追上违章的货车?
(2)在警车追上货车之前,两车间的最大距离是多少?
分析 (1)警车追上违章的货车时,两车位移相等,据此根据运动规律求解追击时间;
(2)警车追上货车时,当两者速度相等时,两车间距离最大,根据运动规律求解最大距离.
解答 解:(1)设警车起动用时为t0,起动后经过时间t追上货车,起动后经时间t′警车达到最大速度.
则v′=at′
解得:$t′=\frac{v′}{a}=\frac{\frac{120}{3.6}}{2}s=16.67s$
假设追击这段时间内警车未达到最大速度,由运动关系可知
$v(t+{t}_{0})=\frac{1}{2}a{t}^{2}$
代入数值解得t=10s<t′
所以上述假设成立,警车追上货车用时10s;
(2)由题意可知,在警车加速到与货车速度相同之前,他们间距离不断在增大,因此当两车速度相等时距离最大,设警车从起动到与货车速度相同时用时为t″则有:
v=at″①
从警车准备起动到与货车同速,货车共向前运动的距离为:
x1=v(t0+t″) ②
警车这段时间内通过的距离为:
${x}_{2}=\frac{1}{2}at{″}^{2}$ ③
代入数据由①②③解得两车间最大距离△x=x1-x2=36m
答:(1)警车从起动后要10s时间才能追上违章的货车;
(2)在警车追上货车之前,两车间的最大距离是36m.
点评 追击问题相遇的条件可以根据位移关系得出,相距最大或最小距离时的条件是两车速度相等,掌握运动规律是正确解题的关键.

练习册系列答案
相关题目
9. 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )| A. | 斜面实验“冲淡”了重力的作用,便于运动时间的测量 | |
| B. | 斜面实验放大了重力的作用,便于测量小球运动的路程 | |
| C. | 通过对斜面实验的观察与计算,直接得到落体运动的规律 | |
| D. | 根据斜面实验结论进行合理的外推,得到落体的运动规律 |
18.以下叙述正确的是( )
| A. | 一群处于n=4能级的氢原子向低能级跃迁时最多可能发出3种不同频率的光子 | |
| B. | β衰变的实质是原子核的内的中子转化成质子和电子 | |
| C. | 核力是一种短程强作用力,作用范围在1.5×10-10m之内 | |
| D. | 太阳辐射的能量主要来自太阳内部的核聚变反应 |
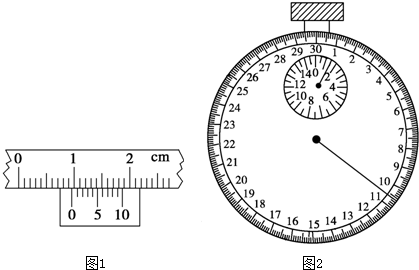
8.小杨同学想利用自由落体运动的装置并结合机械能守恒定律来测定当地的重力加速度,连接好打点计时器的电源后,学生电源面板如图1所示,按下电源开关后发现打点计时器不工作,经检查,打点计时器无故障,线路的连接也没有断路和接触不良等问题.

(1)根据题中信息可判定打点计时器不能正常工作的原因是:计时器接于直流电,应该接于交流电.
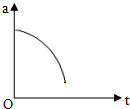
(2)打点计时器不能工作的原因排除后,如图2所示的是小杨同学三次开始打点释放纸带瞬间的照片,请问哪个图中所示的情况操作正确:A.
(3)小杨同学选择操作正确的方式打出的纸带进行分析,选择计数点后通过对纸带记录的数据进行测量和计算,得到了物体下落高度与对应速度值,记录在表中,小杨同学根据实验数据处理的需要,还计算出了速度的平方值填在表格中,请你选择数据在答题纸中的方格纸上建立坐标并描点作图.
(4)请根据你所作的图线,求出当地的重力加速度g=9.75m/s2(保留三位有效数字).经过与当地的重力加速度对比,发现测量值偏小,则产生这种误差的主要原因是有阻力作用,使加速度减小.

(1)根据题中信息可判定打点计时器不能正常工作的原因是:计时器接于直流电,应该接于交流电.
(2)打点计时器不能工作的原因排除后,如图2所示的是小杨同学三次开始打点释放纸带瞬间的照片,请问哪个图中所示的情况操作正确:A.
(3)小杨同学选择操作正确的方式打出的纸带进行分析,选择计数点后通过对纸带记录的数据进行测量和计算,得到了物体下落高度与对应速度值,记录在表中,小杨同学根据实验数据处理的需要,还计算出了速度的平方值填在表格中,请你选择数据在答题纸中的方格纸上建立坐标并描点作图.
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| h(cm) | 6.01 | 11.9 | 18.0 | 25.8 | 34.2 | 39.8 | 44.2 | 52.0 |
| V(m/s) | 1.08 | 1.52 | 1.86 | 2.23 | 2.57 | 2.77 | 2.92 | 3.18 |
| V2(m/s2) | 1.17 | 2.31 | 3.46 | 4.97 | 6.60 | 7.67 | 8.53 | 10.11 |
12. 如图所示,处于真空中的匀强电场与水平方向成15°角,在竖直平面内的直线AB与场强E互相垂直,在A点以大小为v0的初速度水平向右抛出一质量为m、带电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时其速度大小仍为v0,已知A、B、C三点在同一平面内,则在小球由A点运动到C点的过程中( )
如图所示,处于真空中的匀强电场与水平方向成15°角,在竖直平面内的直线AB与场强E互相垂直,在A点以大小为v0的初速度水平向右抛出一质量为m、带电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时其速度大小仍为v0,已知A、B、C三点在同一平面内,则在小球由A点运动到C点的过程中( )
 如图所示,处于真空中的匀强电场与水平方向成15°角,在竖直平面内的直线AB与场强E互相垂直,在A点以大小为v0的初速度水平向右抛出一质量为m、带电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时其速度大小仍为v0,已知A、B、C三点在同一平面内,则在小球由A点运动到C点的过程中( )
如图所示,处于真空中的匀强电场与水平方向成15°角,在竖直平面内的直线AB与场强E互相垂直,在A点以大小为v0的初速度水平向右抛出一质量为m、带电荷量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时其速度大小仍为v0,已知A、B、C三点在同一平面内,则在小球由A点运动到C点的过程中( )| A. | 小球的机械能增加 | B. | 小球的电势能增加 | ||
| C. | 小球的重力势能增加 | D. | C点位于AB直线的右侧 |
 图甲为多用电表的盘面示意图,其中可调部件P为指针定位螺丝,Q为欧姆调零旋钮,K为选择开关,先用它测量一个阻值约为20Ω的电阻,测量步骤如下:
图甲为多用电表的盘面示意图,其中可调部件P为指针定位螺丝,Q为欧姆调零旋钮,K为选择开关,先用它测量一个阻值约为20Ω的电阻,测量步骤如下:

 某质点做直线运动的v-t图象如图示,则0-4s内质点的加速度大小为2.5m/s2;质点停止运动时距离出发点的距离是30m.
某质点做直线运动的v-t图象如图示,则0-4s内质点的加速度大小为2.5m/s2;质点停止运动时距离出发点的距离是30m.