题目内容
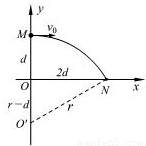
如图所示,真空中有一直角坐标系xOy,M、N分别是y轴和x轴上的两点.该空间内有一匀强电场,方向沿y轴负方向.一质量为m、电荷量为+q的粒子从M点以速度v沿x轴正方向射出,恰能通过N点.已知OM=d,ON=2d,不计粒子重力.(1)求该匀强电场场强E的大小;
(2)若撤去该匀强电场,在该空间加一匀强磁场,仍让这个带电粒子从M点以速度v沿x轴正方向射出,粒子仍通过N点,求所加匀强磁场磁感应强度B的大小和方向.

【答案】分析:(1)根据运动的分解,结合运动学公式与牛顿第二定律,及电场力的表达式,即可求解;
(2)根据左手定则,结合运动的轨迹,从而确定磁场的方向;再由洛伦兹力提供向心力,根据牛顿第二定律与几何关系,从而即可求解.
解答:解:(1)粒子在X轴方向上做匀速直线运动,
所以粒子从M运动到N的时间为t=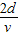
粒子在Y轴方向上做初速度为零的匀加速直线运动,设其加速度为a,
则根据牛顿第二定律有a=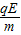
所以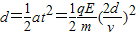
解得: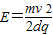
(2)由题意可知,粒子在M点所受洛伦兹力的方向沿Y轴负方向,
根据左手定则可知,所加匀强磁场的方向为:垂直纸面外外.
粒子在匀强磁场中做匀速圆周运动,其轨迹如图所示,O′为轨迹的圆心,其半径为 r.
由勾股定理得:(2d)2+(r-d)2=r2
所以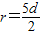
根据牛顿第二定律有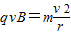
解得: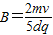
答:(1)则该匀强电场场强E的大小: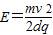 ;
;
(2)则所加匀强磁场磁感应强度B的大小: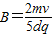 和方向垂直纸面外外.
和方向垂直纸面外外.
点评:考查运动的分解与合成,掌握运动学公式、牛顿第二定律与左手定则的应用,理解几何关系在题中的运用.
(2)根据左手定则,结合运动的轨迹,从而确定磁场的方向;再由洛伦兹力提供向心力,根据牛顿第二定律与几何关系,从而即可求解.
解答:解:(1)粒子在X轴方向上做匀速直线运动,
所以粒子从M运动到N的时间为t=
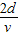
粒子在Y轴方向上做初速度为零的匀加速直线运动,设其加速度为a,
则根据牛顿第二定律有a=
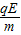
所以
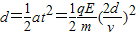
解得:
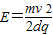
(2)由题意可知,粒子在M点所受洛伦兹力的方向沿Y轴负方向,
根据左手定则可知,所加匀强磁场的方向为:垂直纸面外外.
粒子在匀强磁场中做匀速圆周运动,其轨迹如图所示,O′为轨迹的圆心,其半径为 r.
由勾股定理得:(2d)2+(r-d)2=r2

所以
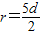
根据牛顿第二定律有
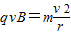
解得:
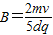
答:(1)则该匀强电场场强E的大小:
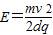 ;
;(2)则所加匀强磁场磁感应强度B的大小:
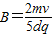 和方向垂直纸面外外.
和方向垂直纸面外外.点评:考查运动的分解与合成,掌握运动学公式、牛顿第二定律与左手定则的应用,理解几何关系在题中的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,真空中有一垂直于纸面向里的匀强磁场,其边界为同心圆,内、外半径分别为r和R.圆心处有一粒子源不断地沿半径方向射出质量为m、电荷量为q的带电粒子,其速度大小为v,不计粒子重力.若
如图所示,真空中有一垂直于纸面向里的匀强磁场,其边界为同心圆,内、外半径分别为r和R.圆心处有一粒子源不断地沿半径方向射出质量为m、电荷量为q的带电粒子,其速度大小为v,不计粒子重力.若 如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( )
如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( ) 如图所示,真空中有一直角坐标系xOy,M、N分别是y轴和x轴上的两点.该空间内有一匀强电场,方向沿y轴负方向.一质量为m、电荷量为+q的粒子从M点以速度v0沿x轴正方向射出,恰能通过N点.已知OM=d,ON=2d,不计粒子重力.
如图所示,真空中有一直角坐标系xOy,M、N分别是y轴和x轴上的两点.该空间内有一匀强电场,方向沿y轴负方向.一质量为m、电荷量为+q的粒子从M点以速度v0沿x轴正方向射出,恰能通过N点.已知OM=d,ON=2d,不计粒子重力. (2010?安丘市模拟)如图所示,真空中有一束平行单色光射入厚度为h的玻璃砖,光与玻璃砖上表面的夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,真空中的光速为c.则
(2010?安丘市模拟)如图所示,真空中有一束平行单色光射入厚度为h的玻璃砖,光与玻璃砖上表面的夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,真空中的光速为c.则 如图所示,真空中有一电子束,以初速度v0沿着垂直场强方向从O点进入电场.以O点为坐标原点,垂直场强方向为x轴,沿场强方向为y轴建立坐标系.沿x轴取A、B、C三点,且OA=AB=BC,再自A、B、C点作y轴的平行线与电子径迹分别交于M、N、P点,则AM:BN:CP=
如图所示,真空中有一电子束,以初速度v0沿着垂直场强方向从O点进入电场.以O点为坐标原点,垂直场强方向为x轴,沿场强方向为y轴建立坐标系.沿x轴取A、B、C三点,且OA=AB=BC,再自A、B、C点作y轴的平行线与电子径迹分别交于M、N、P点,则AM:BN:CP=