题目内容
【题目】如图所示,两平行导轨间距L=0.1 m,足够长的光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上的匀强磁场的磁感应强度B=0.5 T,水平部分没有磁场。金属棒ab的质量m=0.005 kg,电阻r=0.02 Ω,运动中与导轨接触良好,并且始终垂直于导轨,电阻R=0.08 Ω,其余电阻不计,金属棒从斜面上离水平面高h=1.0 m以上任何地方由静止释放,在水平面上滑行的最大距离x都是1.25 m,g=10 m/s2。求:
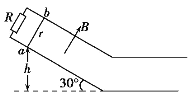
(1)棒在斜面上的最大速度的大小;
(2)棒与水平面间的动摩擦因数;
(3)从高度h=1.0 m处滑下后电阻R上产生的热量。
【答案】(1)v=1.0 m/s (2)μ=0.04 (3)QR=3.8×10-2 J
【解析】
(1)金属棒从离水平面高h=1.0 m以上任何地方由静止释放后,在到达水平面之前已经开始做匀速运动,设匀速时速度为v,则感应电动势:E=BLv
感应电流![]()
安培力:F=BIL,匀速运动时,有:mgsinθ=F
解得:v=1.0 m/s
(2)在水平面上运动时,金属棒所受滑动摩擦力:Ff=μmg
金属棒在摩擦力作用下做匀减速运动,有:Ff=ma
根据速度位移公式:v2=2ax
解得:μ=0.04
(3)下滑的过程中,由动能定理可得:![]()
克服安培力所做的功等于电路中产生的焦耳热,有:![]()
电阻R上产生的热量:![]()
解得:QR=3.8×10-2 J

练习册系列答案
相关题目