题目内容
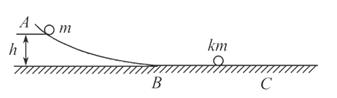
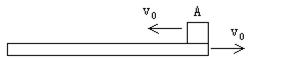
如图所示,一质量为M、长为L的长方形木板B放在光滑水平地面上,在其右端放一质量为m的小木块A,m<M。现以地面为参照系给A、B以大小相等、方向相反的初速度V0,使A开始向左运动、B开始向右运动,最后A刚好没有滑离B板。求:
(1)它们最后的速度大小和方向
(2)A、B系统损失的机械能
(3)小木块A向左运动到达的最远方(从地面上看)离出发点的距离。

(1)它们最后的速度大小和方向
(2)A、B系统损失的机械能
(3)小木块A向左运动到达的最远方(从地面上看)离出发点的距离。
(1) 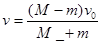 ; (2)
; (2) 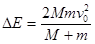 ; (3)
; (3)  。
。
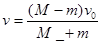 ; (2)
; (2) 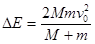 ; (3)
; (3)  。
。试题分析:系统置于光滑水平面,其所受合外力为零,故AB相对滑动时,系统总动量守恒,根据动量守恒定律即可求解;刚好没有滑离,根据动能定理求出相对滑动产生的热量,向左运动到达最远处时速度为0,由动能定理列式,联立方程即可求解。
解答过程:(1)设AB相对静止时速度为V,根据动量守恒定律得:
 (1)
(1)解得:
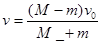 (2)
(2)即它们最后的速度大小为,方向水平向右。
(2)系统损失的机械能全部转化为内能,又最后A刚好没有滑离B板,则由能量守恒定律得:
 (3)
(3)由(2)(3)式解得
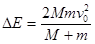 (4)
(4)(3) A向左运动到达最远处时速度为0,对A由动能定理得:
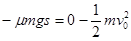 (5)
(5)系统损失的机械能全部转化为内能,则:
 (6)
(6)联立(4)(5)(6)式解得:


练习册系列答案
相关题目
 沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v,已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电力常量为k,则
沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v,已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电力常量为k,则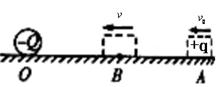
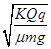
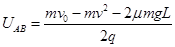
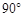 的过程中,以下说法正确的是( )
的过程中,以下说法正确的是( )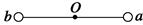
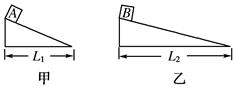
 的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为
的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度为 ,这物体在斜面上上升的最大高度为h,则物体在此过程中
,这物体在斜面上上升的最大高度为h,则物体在此过程中

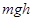

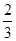 g,在物体下落h的过程中,下列说法中正确的是:( )
g,在物体下落h的过程中,下列说法中正确的是:( )