题目内容
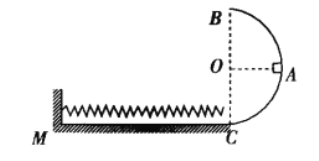
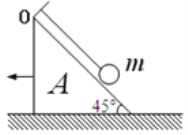
【题目】如图所示,一细线的一端固定于倾角为![]() 的光滑楔形滑块A上的顶端O处,细线另一端拴一质量为m=0.2kg的小球静止在A上。若滑块从静止向左匀加速运动时加速度为a,(取g=10m/s2)则 ( )
的光滑楔形滑块A上的顶端O处,细线另一端拴一质量为m=0.2kg的小球静止在A上。若滑块从静止向左匀加速运动时加速度为a,(取g=10m/s2)则 ( )
A.当a=5m/s2时,细线上的拉力为![]()
B.当a=10 m/s2时,小球受的支持力为![]()
C.当a=10 m/s2时,细线上的拉力为2![]()
D.当a=15m/s2时,若A与小球能相对静止的匀加速运动,则地面对A的支持力一定小于两个物体的重力之和
【答案】AC
【解析】
设加速度为a0时小球对滑块的压力等于零,对小球受力分析,受重力、拉力,根据牛顿第二定律,
水平方向:
F合=Fcos45°=ma0
竖直方向:
Fsin45°=mg
解得:a0=g
A.当a=5m/s2时,小球未离开滑块,
水平方向:
Fcos45°-FNcos45°=ma
竖直方向:
Fsin45°+FNsin45°=mg
解得:
![]() ,
,
故A正确;
BC.当加速度a=10 m/s2时,小球只受绳子拉力和重力,绳子上拉力等于![]() ,故B错误,C正确;
,故B错误,C正确;
D.当加速度a=15 m/s2时,小球离开斜面,由于小球和 斜面体相对静止,对于整体,在竖直方向合力等于0,支持力等于两个物体的重力大小,故D错误。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目