Question

（ 12分）如图所示，AB为水平轨道，A、B间距离s=1m，BCD是半径为R=0.2m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点，整个轨道处于竖直向下的匀强电场中，场强大小为E=。一带正电的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s²)

（1）撤去F时小物块的速度大小；

（2）在半圆形轨道上小物块克服摩擦力做的功。

 

Answer 1

【答案】

（1）v=6m/s                                         

（2）4J                                            

【解析】（1）物体从A运动到B，根据动能定理可得：

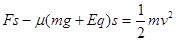                                        （3分）       

求得：v=6m/s                                                     （1分）

（2）物体恰好能到达D点，此时轨道的压力为零，则：

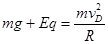                 1                               （3分）

     物体从B点运动到D点，根据动能定理可得：

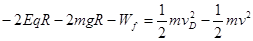        2                     （3分）

联立1、2可得：W_f = 4J                                              （2分）

本题考查动能定理和圆周运动规律的应用，由A到B应用动能定理求得在B点速度大小，物体恰好通过D点，说明只有重力和电场力的合力提供向心力，由此求得D点速度大小，物体有B点到D点，根据动能定理可求得阻力做功大小，主要是通过受力分析确定过程中各力做功的正负，初末状态动能大小