题目内容
9. 如图(a)所示,一个电阻值为R,匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路.线圈的半径为r1.在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图(b)所示.图线与横、纵轴的截距分别为t0和B0.导线的电阻不计.求:
如图(a)所示,一个电阻值为R,匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路.线圈的半径为r1.在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图(b)所示.图线与横、纵轴的截距分别为t0和B0.导线的电阻不计.求:①0至t1时间内通过电阻R1的电流大小和方向
②0至t1时间内通过电阻R1 的电量q
③0至t1时间内电阻R1上产生的热量Q.
分析 ①线圈平面垂直处于匀强磁场中,当磁感应强度随着时间均匀变化时,线圈中的磁通量发生变化,从而导致出现感应电动势,产生感应电流.
②由楞次定律可确定感应电流方向,由法拉第电磁感应定律可求出感应电动势大小.
③产生的热量则是由焦耳定律求出.
解答 解:①由法拉第电磁感应定律:E=n$\frac{△B}{△t}$S=n$\frac{{B}_{0}}{{t}_{0}}$πr22…(1)
由欧姆定律:I=$\frac{E}{3R}$…(2)
联立(1)(2)得:I=$\frac{n{B}_{0}π{{r}_{2}}^{2}}{3R{t}_{0}}$…(3)
由楞次定律可知电流方向:从b到a
②在0至t1时间内电阻R1上产生的电量为:q=It1=n$\frac{△B•π{{r}_{2}}^{2}}{3R}$…(4)
③在0至t1时间内电阻R1上产生的电热为:Q=I22Rt1=$\frac{{n}^{2}{{B}_{0}}^{2}{π}^{2}{{r}_{2}}^{4}}{9{R}^{2}{{t}_{0}}^{2}}$×2Rt1=$\frac{2{n}^{2}{B}_{0}{\;}^{2}{π}^{2}{r}_{2}{\;}^{4}{t}_{1}}{9R{t}_{0}{\;}^{2}}$
答:①通过电阻R1上的电流大小为$\frac{n{B}_{0}π{{r}_{2}}^{2}}{3R{t}_{0}}$,方向为从b到a;
②通过电阻R1上的电量q为n$\frac{△B•π{{r}_{2}}^{2}}{3R}$,
③电阻R1上产生的热量为$\frac{2{n}^{2}{B}_{0}{\;}^{2}{π}^{2}{r}_{2}{\;}^{4}{t}_{1}}{9R{t}_{0}{\;}^{2}}$.
点评 考查楞次定律来判定感应电流方向,由法拉第电磁感应定律来求出感应电动势大小.还可求出电路的电流大小,及电阻消耗的功率.同时磁通量变化的线圈相当于电源.

 如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F发生变化,下列说法中正确的是( )
如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F发生变化,下列说法中正确的是( )| A. | 若拉力突然消失,小球将沿轨迹Pa做直线运动 | |
| B. | 若拉力突然变小,小球将沿轨迹Pc做近心运动 | |
| C. | 若拉力突然变大,小球将沿轨迹Pb做离心运动 | |
| D. | 无论拉力如何变化,小球均沿原轨迹做圆周运动 |
| A. | $\frac{2s}{3}$ | B. | $\frac{s}{t}$ | C. | $\frac{{v}_{0}+{v}_{t}}{2}$ | D. | $\frac{{v}_{t}-{v}_{0}}{2}$ |
| A. | $\frac{70}{3}$m/s | B. | 15 m/s | C. | 5$\sqrt{10}$m/s | D. | 10 m/s |
| A. | 加速度越大,速度变化越大 | |
| B. | 加速度越大,速度变化越快 | |
| C. | 加速度的方向和速度的方向一定相同 | |
| D. | 物体加速度不变,速度也不变 |
 如图甲所示,足够长的木板B静置于光滑水平面上,其上放置小滑块A.木板B受到随时间t变化的水平拉力F作用时,用传感器测出木板B的加速度a,得到如图乙所示的a-F图象,已知g取10m/s2,则( )
如图甲所示,足够长的木板B静置于光滑水平面上,其上放置小滑块A.木板B受到随时间t变化的水平拉力F作用时,用传感器测出木板B的加速度a,得到如图乙所示的a-F图象,已知g取10m/s2,则( )| A. | 滑块A的质量为4kg | B. | 木板B的质量为1kg | ||
| C. | 当F=10N时木板B加速度为4 m/s2 | D. | 滑块A与木板B间动摩擦因数为0.1 |

 如图所示,质量为m=1kg的物体紧靠在粗糙竖直墙面上,以推力F=20N作用在物体上使物体静止,F与水平方向夹角为θ=37°,求物体受竖直墙面的弹力与摩擦力的大小及方向?(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,质量为m=1kg的物体紧靠在粗糙竖直墙面上,以推力F=20N作用在物体上使物体静止,F与水平方向夹角为θ=37°,求物体受竖直墙面的弹力与摩擦力的大小及方向?(sin37°=0.6,cos37°=0.8,g=10m/s2)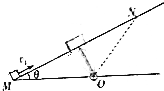 如图所示,绝缘粗糙斜面倾角为θ,斜面下方O点处有一正点电荷,电荷量为Q,带负电的小物体电荷量为q,以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,已知OM=ON,MN=L,小物体在滑动过程中电荷量保持不变,静电力常数为k,求:
如图所示,绝缘粗糙斜面倾角为θ,斜面下方O点处有一正点电荷,电荷量为Q,带负电的小物体电荷量为q,以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,已知OM=ON,MN=L,小物体在滑动过程中电荷量保持不变,静电力常数为k,求: