题目内容
如图所示，一轻质弹簧固定在水平地面上，O点为弹簧原长时上端的位置，一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上，物体压缩弹簧到最低点B 后向上运动．则以下说法正确的是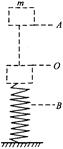
| A．物体落到O点后，立即做减速运动 |
| B．物体从O点运动到B点，动能先增大后减小 |
| C．物体在B点的速度为零，加速度为零 |
| D．在整个过程中，物体m机械能守恒 |
B
解析试题分析：物体从O点运动到B点，先加速到最大速度，此时加速度为零，再向下做减速到零的运动，此时加速度向上达到最大，所以A、C错误，B正确；物体和弹簧系统机械能守恒，D错误。
考点：牛顿第二定律、机械能守恒定律。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案如图所示，穿在水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0，垂直于杆方向施加竖直向上的力F，且F的大小始终与小球的速度成正比，即F=kυ(图中未标出)。已知小球与杆间的动摩擦因数为μ，已知小球运动过程中未从杆上脱落，且F0>μmg.下列说法正确的是：
| A．小球先做加速度减小的加速运动,后做加速度增大的减速运动直到静止 |
| B．小球先做加速度增大的加速运动,后做加速度减小的加速运动，直到最后做匀速运动 |
C．小球的最大加速度为 |
D．恒力F0,的最大功率为 |
蹦级是一种极限体育项目，可以锻炼人的胆量和意志。运动员从高处跳下，弹性绳被拉展前做自由落体运动，弹性绳被拉展后在弹性绳的缓冲作用下，运动员下落一定高度后速度减为零。在这下降的全过程中，下列说法中正确的是
| A．弹性绳拉展前运动员处于失重状态，弹性绳拉展后运动员处于超重状态 |
| B．弹性绳拉展后运动员先处于失重状态，后处于超重状态 |
| C．弹性绳拉展后运动员先处于超重状态，后处于失重状态 |
| D．运动员一直处于失重状态 |
如果把水星和金星绕太阳的运动视为匀速圆周运动，从水星与金星在一条直线上开始计时，若天文学家测得在相同时间内水星转过的角度为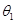
,金星转过的角度为
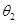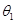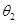(、均为锐角)，则由此条件不可能求得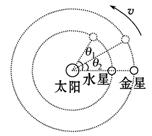
| A．水星和金星的质量之比 |
| B．水星和金星到太阳的距离之比 |
| C．水星和金星绕太阳运动的周期之比 |
| D．水星和金星绕太阳运动的向心加速度大小之比 |
一滑块在水平地面上沿直线滑行，t=0时其速度为2.0m/s。从此刻开始在滑块运动方向上再施加一水平拉力F，力F和滑块的速度v随时间t的变化规律分别如图甲和乙所示。设在第1s内、第2s内、第3s内力F对滑块做功的平均功率分别为P1、P2、P3，则 （ ）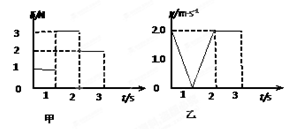
| A．P1>P2>P3 |
| B．P1<P2<P3 |
| C．0~2s内力F对滑块做功为4J |
| D．0~2s内摩擦力对滑块做功为4J |
如右图所示，一根跨越光滑定滑轮的轻绳，两端各有一杂技演员(可视为质点)，a站于地面，b从图示的位置由静止开始向下摆动，运动过程中绳始终处于伸直状态，当演员b摆至最低点时，a刚好对地面无压力，则演员a质量与演员b质量之比为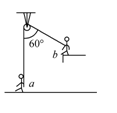
| A．1∶1 | B．2∶1 | C．3∶1 | D．4∶1 |
质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动。已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的
A．线速度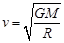 | B．角速度 |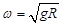
C．运行周期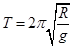 | D．向心加速度 |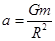
如图所示，小物体从某一高度自由下落，落到竖直在地面的轻弹簧上，在A点物体开始与弹簧接触，到B点物体的速度为零，然后被弹回，则下列说法中正确的是
| A．物体经过A点时速度最大 |
| B．物体从A下落到B的过程中，物体的机械能守恒 |
| C．物体从A下落到B以及从B上升到A的过程中，动能都是先变大后变小 |
| D．物体从A下落到B的过程中的动能和重力势能之和越来越大 |
如右图所示，小球在竖直放置的光滑圆形管道内做圆周运动，内侧壁半径为R，小球半径为r，则下列说法正确的是( )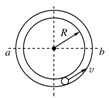
A．小球通过最高点时的最小速度 |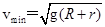
B．小球通过最高点时的最小速度 |
| C．小球在水平线ab以下的管道中运动时，内侧管壁对小球有较小的作用力 |
| D．小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力 |