题目内容
17. 如图所示,用长度相等的轻绳依次连接5000个质量均为m的小球,轻绳的左端固定在天花板上,右端施加一水平力使全部小球静止.若连接天花板的轻绳与水平方向的夹角为45°.则第2014个小球与第2015个小球之间的轻绳与水平方向的夹角α的正切值等于( )
如图所示,用长度相等的轻绳依次连接5000个质量均为m的小球,轻绳的左端固定在天花板上,右端施加一水平力使全部小球静止.若连接天花板的轻绳与水平方向的夹角为45°.则第2014个小球与第2015个小球之间的轻绳与水平方向的夹角α的正切值等于( )| A. | $\frac{2986}{5000}$ | B. | $\frac{2014}{5000}$ | C. | $\frac{2015}{5000}$ | D. | $\frac{2014}{2986}$ |
分析 先以整体为研究对象,由平衡条件求出F的大小,再以2014个到5000个小球组成的整体为研究对象,根据平衡条件求出第2013个小球与2014个小球之间的轻绳与水平方向的夹角α的正切值.
解答  解:以5000个小球组成的整体为研究对象,分析受力情况,如图1所示,因角度为45°
解:以5000个小球组成的整体为研究对象,分析受力情况,如图1所示,因角度为45°
根据平衡条件得拉力等于所用小球的重力:
即:F=5000mg
再以2015个到5000个共2986个小球组成的整体为研究对象,分析受力情况,如图2所示,则由几何关系可得:
tanα=$\frac{2986mg}{F}$=$\frac{2986}{5000}$;
故选:A.
点评 本题的解题关键是选择研究对象,采用整体法与隔离法相结合进行研究,用质点代替物体,作图简单方便.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
12.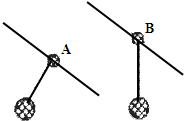 两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
 两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )| A. | A环与杆有摩擦力 | B. | B环与杆无摩擦力 | ||
| C. | A环做的是匀速运动 | D. | B环做的是匀速运动 |
7.站在电梯里的人有“失重”感觉时,电梯可能正在( )
| A. | 加速下降 | B. | 加速上升 | C. | 匀速下降 | D. | 减速下降 |
 小张在显微镜下观察水中悬浮的细微粉笔末的运动,他把小颗粒每隔一定时间的位置记录在坐标纸上(如图所示),于是得出结论,固体小颗粒的无规则运动证明水分子的运动是无规则的,小李不同意小张的结论,他认为:“小颗粒沿着笔直的折线运动,说明水分子在短时间内的运动是规则的,否则小颗粒怎么会沿直线运动?”对此,说说你的看法.
小张在显微镜下观察水中悬浮的细微粉笔末的运动,他把小颗粒每隔一定时间的位置记录在坐标纸上(如图所示),于是得出结论,固体小颗粒的无规则运动证明水分子的运动是无规则的,小李不同意小张的结论,他认为:“小颗粒沿着笔直的折线运动,说明水分子在短时间内的运动是规则的,否则小颗粒怎么会沿直线运动?”对此,说说你的看法. 如图所示,内径均匀的“U”形玻璃管竖直放置,横截面积S=5cm2,右侧管上端封闭,左侧管上端 开口,内有用细线栓住的活塞.两管中均封入长L=11cm的空气柱A和B,活塞上、下表面处的气体压 强均为P=76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm.
如图所示,内径均匀的“U”形玻璃管竖直放置,横截面积S=5cm2,右侧管上端封闭,左侧管上端 开口,内有用细线栓住的活塞.两管中均封入长L=11cm的空气柱A和B,活塞上、下表面处的气体压 强均为P=76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm. 如图所示,绝缘轻杆长L=0.9m,两端固定着带等量异种电荷的小球A、B,A带正电,B带负电,电荷量均为q=6.0×10-6C,质量分别为mA=0.4kg、mB=0.8kg.轻杆可绕过O点的光滑水平轴转动,BO=2AO.整个装置处在水平向右的匀强电场中,电场强度E=5×105N/C.不计一切阻力,取g=10m/s2,一根竖直细线系于杆上OA中点D使杆保持水平,则细线对杆的拉力大小为24N.细线烧断后,小球B的速度最大时杆与竖直方向夹角为37°.
如图所示,绝缘轻杆长L=0.9m,两端固定着带等量异种电荷的小球A、B,A带正电,B带负电,电荷量均为q=6.0×10-6C,质量分别为mA=0.4kg、mB=0.8kg.轻杆可绕过O点的光滑水平轴转动,BO=2AO.整个装置处在水平向右的匀强电场中,电场强度E=5×105N/C.不计一切阻力,取g=10m/s2,一根竖直细线系于杆上OA中点D使杆保持水平,则细线对杆的拉力大小为24N.细线烧断后,小球B的速度最大时杆与竖直方向夹角为37°.
 如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.
如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.