题目内容
4.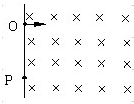 如图,一竖直平面右侧有水平向里的匀强磁场,一带电量为q质量为m的粒子从竖直平面的O以初速度v0水平进入匀强磁场,经过时间T从竖直平面的P点离开磁场,问:
如图,一竖直平面右侧有水平向里的匀强磁场,一带电量为q质量为m的粒子从竖直平面的O以初速度v0水平进入匀强磁场,经过时间T从竖直平面的P点离开磁场,问:(1)粒子带什么电?
(2)OP间的距离是多少?
分析 (1)根据粒子在磁场中偏转方向确定洛伦兹力方向,再由左手定则判断电性.
(2)OP间的距离等于粒子轨道直径,由洛伦兹力等于向心力,求轨道半径,再求OP.
解答 解:(1)粒子进入磁场后向下偏转,所受的洛伦兹力向下,由左手定则知粒子带负电.
(2)粒子在磁场中做匀速圆周运动,设轨道半径为r,由题意可知:
Sop=2r …①
由牛顿第二定律得:
qBv0=m$\frac{{v}_{0}^{2}}{r}$ …②
解①、②得:
Sop=$\frac{2m{v}_{0}}{qB}$ …③
答:(1)粒子带负电.
(2)OP间的距离是$\frac{2m{v}_{0}}{qB}$.
点评 本题是粒子在磁场中圆周运动的轨迹问题,关键是运用几何知识求出半径,再结合洛伦兹力等于向心力处理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.将面积为0.50m2的线圈放在磁感应强度为2.0×10-3T的匀强磁场中,则穿过线圈的磁通量的可能值为( )
| A. | 1.0×10-3Wb | B. | 0.5×10-3Wb | C. | 2.5×10-3Wb | D. | 0.25×10-3Wb |
15.关于电荷的理解正确的是( )
| A. | 元电荷就是电子 | |
| B. | 体积很小的带电体未必就是点电荷 | |
| C. | 检验电荷可以带正电也可以带负电,电量可大可小 | |
| D. | 点电荷类似于质点,是一种理想化模型 |
12.下列关于质点说法正确的是( )
| A. | 运转中的地球不能看作质点,而原子核可以看作质点 | |
| B. | 研究火车通过路旁一根电线杆的时间时,火车可看作质点 | |
| C. | 研究北京奥运会乒乓球男单冠军马琳发球时,不能把乒乓球看成质点 | |
| D. | 研究奥运会三米跳板运动员的跳水动作时,可以将她看作质点 |
19.物体沿一直线运动,下列说法中正确的是( )
| A. | 物体在第一秒末的速度是5 m/s,则物体在第一秒内的位移一定是5 m | |
| B. | 物体在第一秒内的平均速度是5 m/s,则物体在第一秒内的位移一定是5 m | |
| C. | 物体在某段时间内的平均速度是5 m/s,则物体在每一秒内的位移都是5 m | |
| D. | 物体在某段位移内的平均速度是5 m/s,则物体在经过这段位移一半时的速度一定是5 m/s |
9.关于环绕地球做圆周运动的人造卫星,下列说法正确的是( )
| A. | 在同一轨道上运动的不同形状、不同质量的卫星线速度大小也不同 | |
| B. | 卫星绕地球做圆周运动时,其线速度一定不会大于第一宇宙速度 | |
| C. | 为通信需要,可以发射一颗“定位”于南阳市正上方的同步卫星 | |
| D. | 可以发射一颗卫星,使其运动的轨道平面始终与地球上某一经线平面相重合 |
13.河水的流速随离河岸一侧的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,则( )
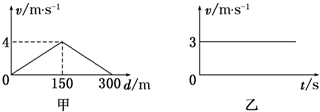

| A. | 船在行驶过程中,船头始终与河岸垂直 | |
| B. | 船在行驶过程中,船头方向要随着水的流速变化而不断调整 | |
| C. | 船渡河的最短时间是60s | |
| D. | 船在河水中航行的轨迹是一条直线 |
14. 图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )
图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )
 图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )
图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )| A. | A点电势较高 | |
| B. | 电子在A点的电势能较大 | |
| C. | 将正电荷从B移动到A,静电力做负功 | |
| D. | A、B两点间的电势差UAB是正的 |
