题目内容
【题目】如图所示，光滑绝缘的正方形水平桌面边长为d=0.48m，离地高度h=1.25m．桌面上存在一水平向左的匀强电场（其余位置均无电场），电场强度E=1×104N/C．在水平桌面上某一位置P处有一质量m=0.01kg，电量q=1×10-6C的带正电小球以初速v0=1m/s向右运动．空气阻力忽略不计，重力加速度g=10m/s2．
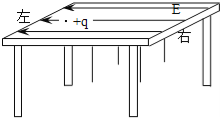
（1）求小球在桌面上运动时的加速度；
（2）P处距右端桌面多远时，小球从开始运动到最终落地的水平距离最大，并求出该最大水平距离．
【答案】（1）1.0m/s2 （2）
m
【解析】（1）对小球受力分析，受到重力、支持力和电场力，重力和支持力平衡，根据牛顿第二定律，有
a=
=
=1.0m/s2 方向：水平向左
（2）球先向右减速，假设桌面足够长，减为零的过程，有
x=
=0.5m，大于桌面边长，故小球一直减速；
设球到桌面右边的距离为x1，球离开桌面后做平抛运动的水平距离为x2，则x总=x1+x2
由v2-v02=-2ax1
代入得 v=
=
设平抛运动的时间为t，根据平抛运动的分位移公式，有
h=
gt2
代入得t=0.5s
水平方向，有x2=vt=0.5
故 x总=x1+0.5
令y=
则 x总=
故，当y=
即x1=
m时，水平距离最大
最大值为：xm=m
即距桌面右端m处放入，有最大水平距离为m
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
