题目内容
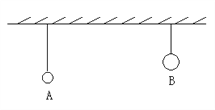
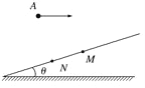
【题目】如图所示,斜面与水平面夹角θ,在斜面上空A点水平抛出两个小球a、b,初速度分别为va、vb,a球恰好垂直打到斜面上M点,而b球落在斜面上的N点,而AN恰好垂直于斜面,则( )
A. a、b两球水平位移之比va∶2vb
B. a、b两球水平位移之比v![]() ∶2v
∶2v![]()
C. a、b两球下落的高度之比v![]() ∶2v
∶2v![]()
D. a、b两球下落的高度之比v![]() :4v
:4v![]()
【答案】BD
【解析】试题分析:平抛运动在某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,结合a、b两球落在斜面上速度与水平方向的夹角关系求出a、b两球的竖直分速度之比,从而得出运动的时间之比和高度之比,结合初速度和时间之比求出水平位移之比.
b球落在N点,位移与斜面垂直,则位移与水平方向的夹角为90°-θ,设此时的速度方向与水平方向的夹角为α,则![]() ,a球速度方向与斜面垂直,速度与水平方向的夹角为
,a球速度方向与斜面垂直,速度与水平方向的夹角为![]() ,可知
,可知![]() ,解得
,解得![]() ,根据
,根据![]() ,则a、b两球下落的高度之比为故
,则a、b两球下落的高度之比为故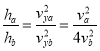 ,C错误D正确,.根据
,C错误D正确,.根据![]() 知,a、b两球的运动时间之比为
知,a、b两球的运动时间之比为![]() ,根据
,根据![]() ,则水平位移之比为
,则水平位移之比为![]() ,A错误B正确.
,A错误B正确.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目