题目内容
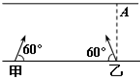
如图所示,甲、乙两船在同一条匀速流动的河流中同时开始渡河,划船速度均为v,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点,则下列判断正确的是( )
| A、甲船比乙船先到达对岸 | B、河水是向右流动 | C、甲乙两船中途不可能相遇 | D、以岸边为参考甲船的比乙船的速度大 |
分析:小船过河的速度为船本身的速度垂直河岸方向的分速度,故要求过河时间需要将船速分解为沿河岸的速度和垂直河岸的速度;要求两船相遇的地点,需要求出两船之间的相对速度,即它们各自沿河岸的速度的和;由于知道了它们过河的时间,故可以求出甲船靠岸的地点.
解答:解:A、小船过河的速度为船本身的速度垂直河岸方向的分速度,故小船过河的速度v
y=vsin60°,故小船过河的时间:t
1=
=
,故甲乙两船到达对岸的时间相同,故A错误;
B、根据题意可知,由于乙船恰好能直达对岸的A点,而两船在到达对岸时相遇,故甲船在A点到达对岸,因此河水向右流动,故B正确;
C、甲船沿河岸方向的速度:v
1+u=vcos60°+u=u+
乙船沿河岸方向的速度:v
2-u=vcos60°-u=
-u
故甲乙两船沿河岸方向的相对速度为:u+
+
-u=v
故两船相遇的时间为:t
2=
H÷v=
=t
1,
故两船在到达对岸时相遇,故C错误,
D、以岸边为参考,根据沿水流方向的位移可知,甲船的比乙船的速度大,故D正确;
故选:BD.
点评:本题考查了运动的合成与分解,相对速度,小船过河问题,注意过河时间由垂直河岸的速度与河宽决定.
练习册系列答案
相关题目
 如图所示,甲、乙两船在同一条匀速流动的河流中同时开始渡河,划船速度均为v,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点,则下列判断正确的是( )
如图所示,甲、乙两船在同一条匀速流动的河流中同时开始渡河,划船速度均为v,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点,则下列判断正确的是( )
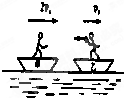 如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速度分别为2v0、v0.为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住,求抛出货物的最小速度.(不计水的阻力)
如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速度分别为2v0、v0.为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住,求抛出货物的最小速度.(不计水的阻力) 如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为u,划船速度均为v,出发时两船相距
如图所示,甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为u,划船速度均为v,出发时两船相距 (1)碘131核不稳定,会发生β衰变,其半衰变期为8天.碘131核的衰变方程:53131I→
(1)碘131核不稳定,会发生β衰变,其半衰变期为8天.碘131核的衰变方程:53131I→