题目内容
 如图所示,位于光滑水平桌面上的小滑块P和Q都可视作质点,质量均为m,Q与轻质弹簧相连.设Q静止,P以某一初速度v0向Q运动并与弹簧发生碰撞,在压缩弹簧的整个碰撞过程中,求:
如图所示,位于光滑水平桌面上的小滑块P和Q都可视作质点,质量均为m,Q与轻质弹簧相连.设Q静止,P以某一初速度v0向Q运动并与弹簧发生碰撞,在压缩弹簧的整个碰撞过程中,求:(1)当弹簧压缩最短时Q的速度为多大?
(2)弹簧具有的最大弹性势能等于多少?
分析:弹簧在压缩的过程中P、Q和弹簧组成的系统动量守恒,可知当压缩最短时P和Q速度相等,根据动量守恒可以求出此时Q的速度为多少;同时在压缩过程中只有弹力做功,系统满足机械能守恒条件,系统的机械能守恒,即弹簧的最大弹性势能等于系统减少的动能.
解答:解:(1)P、Q通过弹簧发生碰撞,当两滑块速度相等时,弹簧压缩到最短,弹性势能最大,设此时共同速度为v,对P、Q(包括弹簧)组成的系统,由动量守恒定律有:
mv0=(m+m)v
解得:v=
v0=
v0
(2)在压缩弹簧的过程中,系统中只有弹簧弹力做功,系统满足机械能守恒条件即系统机械能守恒
所以弹簧增加的弹性势能等于系统减少的动能
即:Epm=
mv02-
(m+m)v2
代入v=
可得:
Epm=
mv02
答:(1)当弹簧压缩最短时Q的速度为
(2)弹簧具有的最大弹性势能等于
m
.
mv0=(m+m)v
解得:v=
| m |
| m+m |
| 1 |
| 2 |
(2)在压缩弹簧的过程中,系统中只有弹簧弹力做功,系统满足机械能守恒条件即系统机械能守恒
所以弹簧增加的弹性势能等于系统减少的动能
即:Epm=
| 1 |
| 2 |
| 1 |
| 2 |
代入v=
| v0 |
| 2 |
Epm=
| 1 |
| 4 |
答:(1)当弹簧压缩最短时Q的速度为
| v0 |
| 2 |
(2)弹簧具有的最大弹性势能等于
| 1 |
| 4 |
| v | 2 0 |
点评:能根据动量守恒条件判断系统动量守恒并能列式求解,能根据机械能守恒条件判断系统机械能守恒并列式求解是解决本题两问的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 (2012?新余模拟)如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.D点位于水桌面最右端,水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离为R,P点到桌面右侧边缘的水平距离为2R.用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后其位移与时间的关系为x=6t-2t2,物块从D点飞离桌面后恰好由P点沿切线落入圆轨道.g=10m/s2,求:
(2012?新余模拟)如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.D点位于水桌面最右端,水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离为R,P点到桌面右侧边缘的水平距离为2R.用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后其位移与时间的关系为x=6t-2t2,物块从D点飞离桌面后恰好由P点沿切线落入圆轨道.g=10m/s2,求: (2012?上海模拟)在动摩擦因数μ=0.2的粗糙绝缘足够长的水平滑漕中,长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B,如图为俯视图(槽两侧光滑).A球的电荷量为+2q,B球的电荷量为-3q(均可视为质点,也不考虑两者间相互作用的库仑力).现让A处于如图所示的有界匀强电场区域MPQN内,已知虚线MP恰位于细杆的中垂线,MP和NQ的距离为3L,匀强电场的场强大小为E=1.2mg/q,方向水平向右.释放带电系统,让A、B从静止开始运动(忽略小球运动中所产生的磁场造成的影响).求:
(2012?上海模拟)在动摩擦因数μ=0.2的粗糙绝缘足够长的水平滑漕中,长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B,如图为俯视图(槽两侧光滑).A球的电荷量为+2q,B球的电荷量为-3q(均可视为质点,也不考虑两者间相互作用的库仑力).现让A处于如图所示的有界匀强电场区域MPQN内,已知虚线MP恰位于细杆的中垂线,MP和NQ的距离为3L,匀强电场的场强大小为E=1.2mg/q,方向水平向右.释放带电系统,让A、B从静止开始运动(忽略小球运动中所产生的磁场造成的影响).求: [物理--选修3-5]
[物理--选修3-5]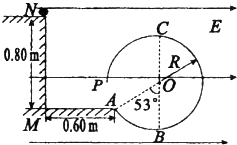 如图所示,光滑绝缘水平台距水平地面高h=0.80m,地面与竖直绝缘光滑圆形轨道在A 点连接.A点距竖直墙壁s=0.60m,整个装置位于水平向右的匀强电场中.现将质量为m=0.1kg、电荷量为g=1×10-3C的带正电荷的小球(可视为质点),从平台上的端点N由静止释放,离开平台N点后恰好切入半径为R=0.4m的绝缘光滑圆形轨道,并沿圆形轨道运动到P点射出.图中O点是圆轨道的圆心,B、C分别是圆形轨道的最低点和最高点.AO与BO之间夹角为53°,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑绝缘水平台距水平地面高h=0.80m,地面与竖直绝缘光滑圆形轨道在A 点连接.A点距竖直墙壁s=0.60m,整个装置位于水平向右的匀强电场中.现将质量为m=0.1kg、电荷量为g=1×10-3C的带正电荷的小球(可视为质点),从平台上的端点N由静止释放,离开平台N点后恰好切入半径为R=0.4m的绝缘光滑圆形轨道,并沿圆形轨道运动到P点射出.图中O点是圆轨道的圆心,B、C分别是圆形轨道的最低点和最高点.AO与BO之间夹角为53°,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: