题目内容
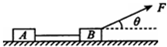
 如图所示,用轻绳连接两个物块A、B,它们的质量分别为mA=10kg、mB=20kg,放在水平固定金属板桌面上(两物体与金属板面间的动摩擦因数相同),在方向与水平方面成θ=37°角斜向上、大小为300N的拉力F作用下,以大小为v0=6.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,用轻绳连接两个物块A、B,它们的质量分别为mA=10kg、mB=20kg,放在水平固定金属板桌面上(两物体与金属板面间的动摩擦因数相同),在方向与水平方面成θ=37°角斜向上、大小为300N的拉力F作用下,以大小为v0=6.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(g取10m/s2,sin37°=0.6,cos37°=0.8)分析:对整体分析,根据共点力平衡求出动摩擦因数的大小,然后隔离对A分析,根据牛顿第二定律求出物块A的加速度大小,运用速度位移公式求出物块在水平面上滑行的距离.
解答:解:对整体研究,有:Fcosθ=f.
f=μN=μ[(mA+mB)g-Fsinθ]
联立两式解得:μ=0.5
隔离对A分析,根据牛顿第二定律:a=
=μg=5m/s2
则物块A在水平地面上滑行的位移:x=
=
m=3.6m.
答:剪断轻绳后物块A在水平地面上滑行的距离为3.6m.
f=μN=μ[(mA+mB)g-Fsinθ]
联立两式解得:μ=0.5
隔离对A分析,根据牛顿第二定律:a=
| μmg |
| m |
则物块A在水平地面上滑行的位移:x=
| v02 |
| 2a |
| 36 |
| 10 |
答:剪断轻绳后物块A在水平地面上滑行的距离为3.6m.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,注意整体法和隔离法的使用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
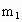 、
、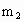 的A、B两物体,在光滑的水平面上先后用大小相同的恒力F,向右拉物体A或向左拉物体B,使A、B一起做初速度为零的匀加速直线运动.第一种情况下,绳
的A、B两物体,在光滑的水平面上先后用大小相同的恒力F,向右拉物体A或向左拉物体B,使A、B一起做初速度为零的匀加速直线运动.第一种情况下,绳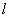 的张力为
的张力为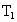 ;第二种情况下,绳
;第二种情况下,绳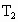 ,请用牛顿力学方法分析和讨论
,请用牛顿力学方法分析和讨论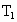 和
和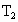 的大小关系.
的大小关系.
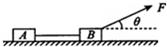 如图所示,用轻绳连接两个物块A、B,它们的质量分别为mA=10kg、mB=20kg,放在水平固定金属板桌面上(两物体与金属板面间的动摩擦因数相同),在方向与水平方面成θ=37°角斜向上、大小为300N的拉力F作用下,以大小为v0=6.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,用轻绳连接两个物块A、B,它们的质量分别为mA=10kg、mB=20kg,放在水平固定金属板桌面上(两物体与金属板面间的动摩擦因数相同),在方向与水平方面成θ=37°角斜向上、大小为300N的拉力F作用下,以大小为v0=6.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(g取10m/s2,sin37°=0.6,cos37°=0.8)