题目内容
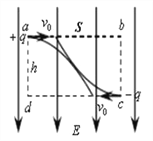
【题目】如图,有一矩形区域abcd,水平边ab长为![]() ,竖直边ad长为h=1m. 质量均为m、带电量分别为+q和-q的两粒子,
,竖直边ad长为h=1m. 质量均为m、带电量分别为+q和-q的两粒子, ![]() .当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率
.当矩形区域只存在场强大小为E=10N/C、方向竖直向下的匀强电场时,+q由a点沿ab方向以速率![]() 进入矩形区域,轨迹如图。当矩形区域只存在匀强磁场时-q由c点沿cd方向以同样的速率
进入矩形区域,轨迹如图。当矩形区域只存在匀强磁场时-q由c点沿cd方向以同样的速率![]() 进入矩形区域,轨迹如图。不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心。则( )
进入矩形区域,轨迹如图。不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心。则( )
A. 由题给数据,初速度![]() 可求
可求
B. 磁场方向垂直纸面向外
C. -q做匀速圆周运动的圆心在b点
D. 两粒子各自离开矩形区域时的动能相等。
【答案】AC
【解析】试题分析:因为粒子通过矩形区域的几何中心,可知沿电场方向上的距离y=![]() ="0.5" m,垂直电场方向上的距离x=
="0.5" m,垂直电场方向上的距离x=![]() =
=![]() m,根据y=
m,根据y=![]() at2=
at2=![]()
![]() ,可以求出初速度的大小,故A正确;﹣q由c点沿cd方向以同样的速率v0进入矩形区域,根据洛伦兹力的方向,结合左手定则知,磁场方向垂直纸面向里,故B错误;因为圆周运动的轨迹经过矩形区域的几何中心,设中心为O,根据几何关系知,bO=
,可以求出初速度的大小,故A正确;﹣q由c点沿cd方向以同样的速率v0进入矩形区域,根据洛伦兹力的方向,结合左手定则知,磁场方向垂直纸面向里,故B错误;因为圆周运动的轨迹经过矩形区域的几何中心,设中心为O,根据几何关系知,bO=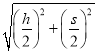 =
=![]() ="1" m,可知矩形区域几何中心到b点的距离等于bc的距离,知b点为圆周运动的圆心,故C正确;电荷在电场中做类平抛运动,速度增大,在磁场中做匀速圆周运动,速度大小不变,可知离开区域区域时动能不等,故D错误。
="1" m,可知矩形区域几何中心到b点的距离等于bc的距离,知b点为圆周运动的圆心,故C正确;电荷在电场中做类平抛运动,速度增大,在磁场中做匀速圆周运动,速度大小不变,可知离开区域区域时动能不等,故D错误。

练习册系列答案
相关题目