题目内容
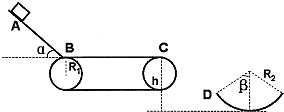 如图为一传送货物的装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带运输后,最后抛入固定于水平地面上的圆弧形槽内.已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m.圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°.当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内.当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求:
如图为一传送货物的装置,倾角为α=53°的斜面AB与水平传送带在B处由一光滑小圆弧平滑衔接,可看作质点的货物从斜面上A点由静止下滑,经长度为S1的传送带运输后,最后抛入固定于水平地面上的圆弧形槽内.已知物体与斜面、传送带间的滑动摩擦因数均为μ=0.5,传送带两皮带轮的半径均为R1=0.4m,传送带上表面BC离地的高度h=1.2m.圆弧槽半径R2=1m,两边缘与圆心连线与竖直方向的夹角均为β=53°.当传送带静止时,将货物在斜面上离B点S2远处静止释放,货物脱离传送带后刚好沿圆弧槽左边缘D点的切线方向飞入槽内.当传送带顺时针转动时,无论传送带转多快,货物也不会从圆弧槽右边缘飞出,求:(1)传送带静止时,货物到达D点时的速度大小.
(2)求S1、S2的值应满足的关系.(sin53°=0.8,cos53°=0.6 )
分析:(1)物体离开C后做平抛运动,应用运动的合成与分解、动能定理可以求出物体到达C、D两点的速度,由牛顿第二定律求出物体做平抛的临界速度,然后求出货物到达D点的速度.
(2)应用动能定理与平抛运动知识求出S1、S2的值应满足的关系.
(2)应用动能定理与平抛运动知识求出S1、S2的值应满足的关系.
解答:解:(1)物体到达C点的速度为v1,到达D点的速度为v2,
方向与水平方向成53°,v1=v2cos53°①,
从C到D货物机械能守恒,由机械能守恒定律得:
mgh+
mv12=mgR2(10cos53°)+
mv22 ②,
解得:v1=3m/s,v2=5m/s,
在C点,货物脱离传送带做平抛运动的临界条件为:mg=
③,
由③解得,v0=
=2m/s;
由于v1>v0,说明物体可以从C点开始做平抛运动,
货物通过D点的速度大小为5m/s;
(2)传送带静止时,货物到达C点的速度为v1=3m/s,
由动能定理得:mgs2sin53°-μmgs2cos53°-μmgs1=
④,
由④解得,s2-s1=0.9m ⑤,
传送带足够大时,货物一直在传送带上加速,最终在C点做平抛运动,
临界状态为恰好到达圆弧槽右边缘,根据平抛运动知识可得:
h-R(1-cos53°)=
gt2 ⑥,
由⑥解得,t=0.4s,
射程s=v1t+2R2sin53°=2.8m ⑦,
由⑦可解得平抛运动的初速度v3=
=7m/s;
因为货物不会从圆弧槽右边缘飞出,
由动能定理得:mgs2sin53°-μmgs2cos53°+μmgs2=EKC ⑧,
EKC≤
⑨,
由⑧⑨可得,s1+s2≤4.9m ⑩,
综上⑤⑩,s1与s2应满足:s2-s1=0.9m,且s1+s2≤4.9m;
答:(1)传送带静止时,货物到达D点时的速度大小为5m/s.
(2)S1、S2的值应满足的关系为s2-s1=0.9m,且s1+s2≤4.9m.
方向与水平方向成53°,v1=v2cos53°①,
从C到D货物机械能守恒,由机械能守恒定律得:
mgh+
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=3m/s,v2=5m/s,
在C点,货物脱离传送带做平抛运动的临界条件为:mg=
m
| ||
| R1 |
由③解得,v0=
| gR |
由于v1>v0,说明物体可以从C点开始做平抛运动,
货物通过D点的速度大小为5m/s;
(2)传送带静止时,货物到达C点的速度为v1=3m/s,
由动能定理得:mgs2sin53°-μmgs2cos53°-μmgs1=
m
| ||
| 2 |
由④解得,s2-s1=0.9m ⑤,
传送带足够大时,货物一直在传送带上加速,最终在C点做平抛运动,
临界状态为恰好到达圆弧槽右边缘,根据平抛运动知识可得:
h-R(1-cos53°)=
| 1 |
| 2 |
由⑥解得,t=0.4s,
射程s=v1t+2R2sin53°=2.8m ⑦,
由⑦可解得平抛运动的初速度v3=
| s |
| t |
因为货物不会从圆弧槽右边缘飞出,
由动能定理得:mgs2sin53°-μmgs2cos53°+μmgs2=EKC ⑧,
EKC≤
m
| ||
| 2 |
由⑧⑨可得,s1+s2≤4.9m ⑩,
综上⑤⑩,s1与s2应满足:s2-s1=0.9m,且s1+s2≤4.9m;
答:(1)传送带静止时,货物到达D点时的速度大小为5m/s.
(2)S1、S2的值应满足的关系为s2-s1=0.9m,且s1+s2≤4.9m.
点评:本题难度较大,分析清楚物体的运动过程是正确解题的前提与关键,应用动能定理、平抛运动知识即可正确解题.

练习册系列答案
相关题目
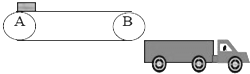 如图所示为某工厂装载货物的原理示意图,设传送AB 的长度为8m,货物与传送带的动摩擦力因数为0.6,货物以初速度10m/s滑至传送带的A 端,车厢长为12m,车厢的顶部到B 顶端的高度差为1.25m,通过调节传送带(瞬时针)的速度可合理地将车厢装满以实现自动装货,则下列说法中正确的是( )
如图所示为某工厂装载货物的原理示意图,设传送AB 的长度为8m,货物与传送带的动摩擦力因数为0.6,货物以初速度10m/s滑至传送带的A 端,车厢长为12m,车厢的顶部到B 顶端的高度差为1.25m,通过调节传送带(瞬时针)的速度可合理地将车厢装满以实现自动装货,则下列说法中正确的是( )| A、车厢到B 的水平距离至少1m 时,货物才能装进车厢 | B、若传送带逆时针转动时,货物不可能装进车厢 | C、只要传带的速度足够大,货物就可到达车厢的右端 | D、若要货物达到车厢的右端,司机需要把车向左移动一段距离 |
