题目内容
如图，光滑的
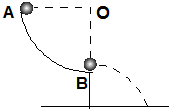
圆形轨道AB，OA水平．有光滑小球m自A点自由下滑过B点后离
开轨道，则在B处前后的瞬间小球的加速度大小之比为______．
| 1 |
| 4 |
开轨道，则在B处前后的瞬间小球的加速度大小之比为______．
机械能守恒定律可得：
mgR=
mv2，
解得：
v2=2gR，
故此时向心加速度为：
a=
=2g，
而小球过B点后做平抛加速度为重力加速度g，
故在B处前后的瞬间小球的加速度大小之比为：
2g：g=2：1．
故答案为：2：1．
mgR=
| 1 |
| 2 |
解得：
v2=2gR，
故此时向心加速度为：
a=
| v2 |
| R |
而小球过B点后做平抛加速度为重力加速度g，
故在B处前后的瞬间小球的加速度大小之比为：
2g：g=2：1．
故答案为：2：1．
练习册系列答案
相关题目
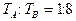，则轨道半径之比和运动速率之比分别为（）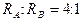
，
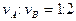
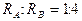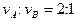
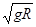
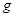
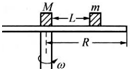
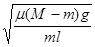
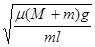
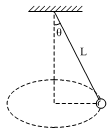
下端连接一只小球，小球与
地面间的距离可以忽略（但小球不受地面支持力）且处于静止状态．现给小球一沿水平方向的初速度，使其开始在竖直平面内做圆周运动。设小球到达最高点时轻绳突然断开，已知最后小球落在距
初
始位置水平距离为4R