题目内容
9.下列说法正确的是 ( )| A. | 只要知道气体的摩尔体积和阿伏伽德罗常数,就可以算出气体分子的体积 | |
| B. | 在一定温度下,悬浮在液体中的固体微粒越小,布朗运动就越明显 | |
| C. | 一定质量的理想气体压强不变时,气体分子单位时间内对器壁单位面积的平均碰撞次数随着温度升高而减少 | |
| D. | 一定温度下,水的饱和汽的压强是一定的 | |
| E. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间只有引力,没有斥力,所以液体表面具有收缩的趋势 |
分析 阿伏伽德罗常数是指1摩尔气体含有分子个数;布朗运动是指微粒在分子撞击下的运动,微粒越大运动越不明显;永动机不违反能量守恒定律,但不可制成;理想气体的分子势能不变;分子间既有引力又有斥力,当间距小于平衡位置时,斥力较显著
解答 解:A、摩尔体积除以阿伏伽德罗常数算出的是气体分子占据的空间,气体分子间的空隙很大,所以气体分子占据的空间不等于气体分子的体积.故A错误;
B、悬浮在液体中的固体微粒越小,来自各方向的撞击抵消的越少,则布朗运动就越明显.故B正确;
C、一定质量的理想气体压强不变时,温度升高,则体积一定减小;故气体分子单位时间内对器壁单位面积的平均碰撞次数随着温度升高而减少;故C正确;
D、水的饱和汽压和温度有关,一定温度下,水的饱和汽的压强是一定的;故D正确;
E、分子间同时存在引力和斥力,液体分子存在表面张力的原因是引力大于斥力;对外表现为引力;从而使且面收缩;故E错误;
故选:BCD.
点评 知道固体、液体、气体分子的模型及运动特点;知道布朗运动其实是分子撞击布朗颗粒而产生的运动;知道温度是分子平均动能的标志,注意平时加强识记

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.两种单色光由水中以相同的入射角射向真空时,单色光1部分折射入真空,单色光2发生了全反射,用n1、n2表示水对两单色光的折射率,v1、v2分别表示两种单色光在水中的传播速度,λ1、λ2分别表示两种单色光在水中的波长,λ10、λ20分别表示两种单色光在真空中的波长,则( )
| A. | n1>n2 | B. | v1<v2 | C. | λ1>λ2 | D. | λ1=$\frac{{λ}_{10}}{{n}_{1}}$ |
20.下列说法正确的是( )
| A. | 泊松亮斑是光的衍射现象,玻璃管中的气泡看起来特别明亮是光的全反射现象 | |
| B. | 在电磁波接收过程中,使声音信号或图象信号从高频电磁波中还原出来的过程叫调制 | |
| C. | 一简谐横波以速度v沿x轴正方向传播,t=0时传播到坐标原点,此质点正从平衡位置以速度v0向下振动.已知质点的振幅为A,振动角频率为ω,则x轴上横坐标为$\frac{3}{4}$λ处质点的振动方程为y=-Asinω(t-$\frac{3λ}{4v}$) | |
| D. | 在光的双逢干涉实验中,若仅将入射光由绿光改为红光,则干涉条纹间距变窄 | |
| E. | 真空中的光速在不同的惯性参考系中都是相同的,与光源、观察者间的相对运动没有关系 |
17.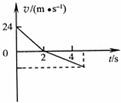 将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )
将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )
 将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )
将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2.下列说法中正确的是( )| A. | 小球上升与下落所用时间之比为2:3 | |
| B. | 小球下落过程,处于超重状态 | |
| C. | 小球上升过程中克服阻力做功的功率大于下降过程克服阻力做功的功率 | |
| D. | 小球上升过程中机械能的损失大于下落过程中的机械能损失 |
14.如图所示为两物体a、b从同一位置沿同一直线运动的速度图象,下列说法正确的是( )
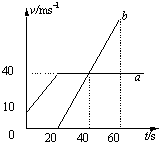

| A. | 第40s时,两物体a,b相遇 | |
| B. | 第60s时,两物体a,b相遇 | |
| C. | 第20s和第60s时,两物体a,b的间距相等 | |
| D. | a,b加速时,物体a的加速度大于物体b的加速度 |
1.对爱因斯坦光电效应方程EK=hv-W,下面的理解正确的有( )
| A. | 只要是用同种频率的光照射同一种金属,那么从金属中逸出的所有光电子都会具有同样的初动能EK | |
| B. | 式中的W表示每个光电子从金属中飞出过程中克服金属中正电荷引力所做的功 | |
| C. | 逸出功W和极限频率v0之间应满足关系式W=hv0 | |
| D. | 光电子的最大初动能和入射光的频率不是成正比 |
18.下列说法正确的是( )
| A. | 在“用油膜法估测分子大小”的实验中,油脂分子的直径等于油酸酒精溶液的体积除以相应油脂膜的面积 | |
| B. | 悬浮在液体中的固体颗粒越小,液体的温度越高,布朗运动越剧烈 | |
| C. | 质量,温度都相同的氢气和氧气,分子的平均功能不相同 | |
| D. | 液晶的光学性质与某些晶体相似,具有各向异性 |
19.火星探测已成为世界各国航天领域的研究热点.现有人想设计发射一颗火星的同步卫星.若已知火星的质量M,半径R0,火星表面的重力加速度g0自转的角速度ω0,引力常量G,则同步卫星离火星表面的高度为( )
| A. | $\root{3}{{\frac{{{g_0}R_0^2}}{ω_0^2}}}-{R_0}$ | B. | $\root{3}{{\frac{{{g_0}R_0^2}}{ω_0^2}}}$ | ||
| C. | $\root{3}{{\frac{GM}{ω_0^2}}}-{R_0}$ | D. | $\root{3}{{\frac{GM}{ω_0^2}}}$ |
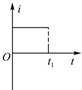
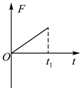
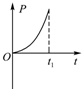
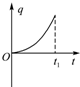
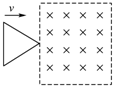 如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向里,等边三角形金属框电阻为R,边长是L,自线框从左边界进入磁场时开始计时,在外力作用下以垂直于磁场边界的恒定速度v进入磁场区域,t1时刻线框全部进入磁场.规定逆时针方向为感应电流i的正方向.外力大小为F,线框中电功率的瞬时值为P,在这段时间内通过导体某横截面的电荷量为q,其中C、D图象为抛物线.则这些物理量随时间变化的关系可能正确的是( )
如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向里,等边三角形金属框电阻为R,边长是L,自线框从左边界进入磁场时开始计时,在外力作用下以垂直于磁场边界的恒定速度v进入磁场区域,t1时刻线框全部进入磁场.规定逆时针方向为感应电流i的正方向.外力大小为F,线框中电功率的瞬时值为P,在这段时间内通过导体某横截面的电荷量为q,其中C、D图象为抛物线.则这些物理量随时间变化的关系可能正确的是( )