Question

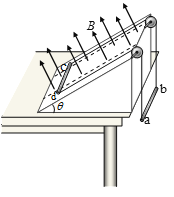
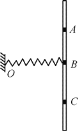
【题目】如图所示，光滑竖直杆固定，杆上套一质量为m的环，环与轻弹簧一端相连，弹簧的另一端固定在O点，O点与B点在同一水平线上，BC>AB，AC=h，环从A处由静止释放运动到B点时弹簧仍处于伸长状态，整个运动过程中弹簧始终处于弹性限度内，重力加速度为g，环从A处开始运动时的加速度大小为2g，则在环向下运动的过程中（　　）

A.环在B处的加速度大小为0B.环在C处的速度大小为

C.环从B到C一直做加速运动D.环的速度最大的位置在B、C两点之间

Answer 1

【答案】D

【解析】

A．环在处水平方向合外力为0，竖直方向上只受重力，所加速度为，A错误；

B．环在运动过程中，OC的长度大于OA的长度，因此弹簧从A点到C点伸长量变大，弹性势能增加，如果物体的重力势能全部转化为动能则有

可得物体的速度为，但是物体的重力势能转化为动能和弹性势能，因此速度小于，B错误；

CD．环在处，根据牛顿第二定律

弹力在竖直方向的分力

环经过点向下做加速度减小的加速运动，滑动至距离点处时，弹簧的伸长量与在处大小相等，所以弹簧弹力在竖直方向的分力与重力等大反向，加速度为0，此时速度最大，之后环做减速运动，因为，所以环的速度最大的位置在B、C两点之间，环从B到C先加速后减速，C错误，D正确。

故选D。