题目内容
（16分）在如图所示的直角坐标中，x轴的上方有与x轴正方向成45°角的匀强电场，场强的大小为E＝
×104V/m。x轴的下方有垂直于xOy面的匀强磁场，磁感应强度的大小为 B＝1×10－2T。把一个比荷为
C/kg的正电荷从y轴上坐标为（0，1）的A点处由静止释放。电荷所受的重力忽略不计，求：（1）电荷从释放到第一次进入磁场时所用的时间t；
（2）电荷在磁场中的偏转半径；
（3）电荷第三次到达x轴上的位置。
（16分）解：（1）带电粒子沿电场方向做匀加速直线运动，由牛顿第二定律得：Eq=ma
到进入磁场的位移为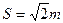
而 
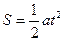
代入数据得：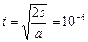
s （4分）
（2）射入磁场时的速度为：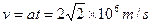
方向与电场线方向相同
由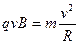
得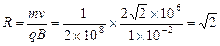
m （4分）
（3）第二次到达X轴的坐标为（-1，0）；设第三次到达X轴时与第二次到达轴的距离为L，由于射入电场时速度与电场方向垂直，做类平抛运动。
则有：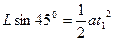
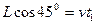（4分）
解得L=8m
电荷第三次到达x轴上的点的坐标为（7，0）（4分）
到进入磁场的位移为
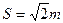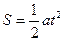
而 代入数据得：
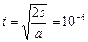s （4分）（2）射入磁场时的速度为：
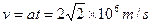方向与电场线方向相同由
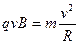得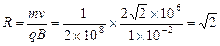m （4分）（3）第二次到达X轴的坐标为（-1，0）；设第三次到达X轴时与第二次到达轴的距离为L，由于射入电场时速度与电场方向垂直，做类平抛运动。
则有：
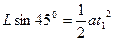
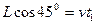（4分）解得L=8m
电荷第三次到达x轴上的点的坐标为（7，0）（4分）
略
练习册系列答案
相关题目
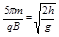，则小球落点与抛出点A的水平位移S是 （ ）
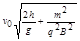
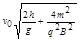
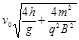
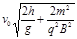
的两块正对的平行金属板P、Q，板长
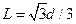两板带等量异种电荷，上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出)，其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入，并恰好从下极板边缘射出，又经过在矩形有界磁场中的偏转，最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求：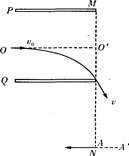
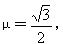除此之外，不记其他损耗。求电动机由于传送工件多消耗的电能。（取g＝10 m/s2）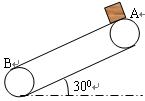
0.6，cos37°=0.8，g=10m/s2）
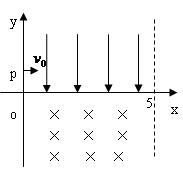
。第四象限有垂直平面向里的匀强磁场，磁感应强度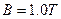
。它们的右边界为x=5.0m，今有一个质量
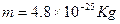,电荷量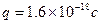
的带正电粒子（不计重力），在y轴上距坐标原点d=0.3m的p处以初速度
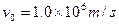沿x轴正方向射入匀强电场。求：带电粒子在电场和磁场中运动的总时间t.