题目内容
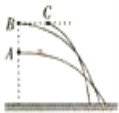
【题目】如图所示,光滑轨道由AB、BCDE两段细圆管平滑连接组成,其中AB段水平,BCDE段为半径为R的四分之三圆弧,圆心O及D点与AB等高,整个轨道固定在竖直平面内,现有一质量为m,初速度v0=![]() 的光滑小球水平进入圆管AB,设小球经过轨道交接处无能量损失,圆管孔径远小于R,则(小球直径略小于管内径)( )
的光滑小球水平进入圆管AB,设小球经过轨道交接处无能量损失,圆管孔径远小于R,则(小球直径略小于管内径)( )
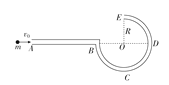
A. 小球到达C点时的速度大小vC=![]()
B. 小球能通过E点且抛出后恰好落至B点
C. 无论小球的初速度v0为多少,小球到达E点时的速度都不能为零
D. 若将DE轨道拆除,则小球能上升的最大高度与D点相距2R
【答案】B
【解析】A、小球从A至C过程,由机械能守恒定律得(以AB为参考平面): ![]() ,将
,将![]() 代入得:
代入得: ![]() ,故A错误;
,故A错误;
B、从A至E过程,由机械能守恒定律得: ![]() ,解得
,解得 ![]()
从E点开始小球做平抛运动,则由![]() ,小球能正好平抛落回B点,故B正确;
,小球能正好平抛落回B点,故B正确;
C、因为是圆弧管,内管壁可提供支持力,所以小球在E点速度可以为零,故C错误;
D、若将DE轨道拆除,设小球能上升的最大高度为h,由机械能守恒得: ![]() ,解得
,解得![]() ,故D错误。
,故D错误。

练习册系列答案
相关题目