题目内容
(16分)
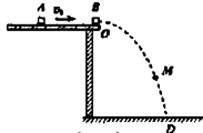
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。
(1)已知滑块质量为m,碰撞时间为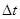 ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
(1)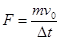
(2)a.A下滑到任意一点的动量总和是小于B平抛经过该点的动量。
b.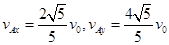
【解析】(1)滑动A与B正碰,满足
mvA-mVB=mv0 ①
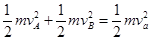 ②
②
由①②,解得vA=0, vB=v0,
根据动量定理,滑块B满足 F·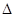 t=mv0
解得
t=mv0
解得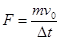
(2)a.设任意点到O点竖直高度差为d.
A、B由O点分别运动至该点过程中,只有重力做功,所以机械能守恒。
选该任意点为势能零点,有
EA=mgd,EB= mgd+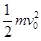 由于p=
由于p= ,有
,有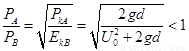
即 PA<PB[
A下滑到任意一点的动量总和是小于B平抛经过该点的动量。
b.以O为原点,建立直角坐标系xOy,x轴正方向水平向右,y轴正方向竖直向下,则对B有
x=v0t·y= gt2
B的轨迹方程
y=
gt2
B的轨迹方程
y=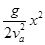
在M点x=y,所以 y=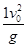
 ③
③
因为A、B的运动轨迹均为OD曲线,故在任意一点,两者速度方向相同。设B水平和竖直分速度大小分别为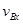 和
和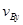 ,速率为vB;A水平和竖直分速度大小分别为
,速率为vB;A水平和竖直分速度大小分别为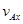 和
和 ,速率为vA,则
,速率为vA,则
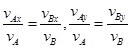 ④
④
B做平抛运动,故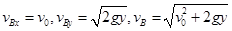 ⑤
⑤
对A由机械能守恒得vA=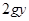 ⑥
⑥
由④⑤⑥得 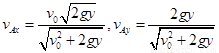
将③代入得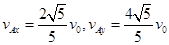

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 (2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示.
(2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示. (2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。 (2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨道完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。