题目内容
13.一架飞机在高度为10km上空飞行,机上乘客看见太阳升起,估计在飞机正下方地面上的观察者要经过多少时间才可以看见太阳?分析 设站在地面上的观察者经过时间t看见太阳,t为此时地球绕地轴转过角α(如图所示)所需要的时间,根据几何关系求出角度α,再根据t=$t=\frac{α}{ω}=\frac{α}{\frac{2π}{T}}$求解,难度较大.
解答 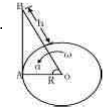 解:设站在地面上的观察者经过时间t看见太阳,t为此时地球绕地轴转过角α(如图所示)所需要的时间,
解:设站在地面上的观察者经过时间t看见太阳,t为此时地球绕地轴转过角α(如图所示)所需要的时间,
在直角△AB0中,飞机离地面的高度h=10km,地球半径R=6400km,则
$\frac{R}{R+h}=cosα$
$\frac{h}{R}=\frac{1-cosα}{cosα}=tanα•tan\frac{α}{2}$
因为α很小,所以tanα=α,$tan\frac{α}{2}=\frac{α}{2}$,于是
$\frac{h}{R}=\frac{1}{2}{α}^{2}$,$α=\sqrt{\frac{2h}{R}}$,
$t=\frac{α}{ω}=\frac{α}{\frac{2π}{T}}=\frac{\sqrt{\frac{2h}{R}}}{\frac{2π}{T}}=13min$(式中ω是地球自转角速度,T=24小时)
答:在飞机正下方地面上的观察者要经过13min时间才可以看见太阳.
点评 本题主要考查了匀速圆周运动时间的求法,知道时间t=$\frac{θ}{2π}T$,注意几何关系在解题中的应用,难度较大.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
1.“嫦娥三号”在环月圆轨道上做匀速圆周运动,向心力为F,动能为Ek;关于它们的变化情况,正确的是 ( )
| A. | F不变,Ek不变 | B. | F不变,Ek变化 | C. | F变化,Ek不变 | D. | F变化,Ek变化 |
18.2013年夏,四川北川老县城地震遗址遭遇50年最强洪水,武警战士驾驶冲锋舟营救被困群众,某段时间内冲锋舟的运动规律为x=-2t2-6t,y=1.5t2+4t,xOy为直角坐标系,则下列说法正确的是( )
| A. | 冲锋舟在x方向的分运动是匀减速直线运动 | |
| B. | 冲锋舟的运动是匀变速直线运动 | |
| C. | 冲锋舟的运动是匀变速曲线运动 | |
| D. | 冲锋舟的运动开始为直线运动后变为曲线运动 |
 光滑水平面上放有如图所示的用绝缘材料制成的“┘”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦系数为μ,qE=2μmg,整个装置处于场强为E的水平匀强电场中,初始时刻,滑板与物体都静止,试求:
光滑水平面上放有如图所示的用绝缘材料制成的“┘”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦系数为μ,qE=2μmg,整个装置处于场强为E的水平匀强电场中,初始时刻,滑板与物体都静止,试求: 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为2m,木板质量m,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.设木板足够长,重物始终在木板上.重力加速度为g.求
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为2m,木板质量m,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.设木板足够长,重物始终在木板上.重力加速度为g.求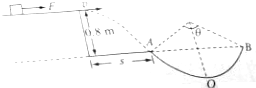 一质量m=2kg的物体,由静止开始,在水平拉力F的作用下在距地面高度h=0.8m的光滑平台上运动,一段时间后,撤去力F,物体继续运动到达平台右端后离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,平台右端到A点的水平距离s=1.2m,取g=10m/s2,求:
一质量m=2kg的物体,由静止开始,在水平拉力F的作用下在距地面高度h=0.8m的光滑平台上运动,一段时间后,撤去力F,物体继续运动到达平台右端后离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,平台右端到A点的水平距离s=1.2m,取g=10m/s2,求: 水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.
水平面上固定着直角支架ABC,支架所在平面与水平面垂直,在AC和BC杆上分别套有质量为m1和m2的光滑圆环,且m1和m2用轻质细线相连,如图所示,已知AC与水平面的夹角为θ,求m1和m2平衡后,细线上的拉力.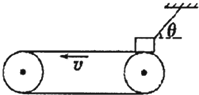 如图所示,质量m=4kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.2,传送带的长度l=6m,当传送带以v=4m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°.已知:sin37°=0.6,cos37°=0.8.求:
如图所示,质量m=4kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.2,传送带的长度l=6m,当传送带以v=4m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°.已知:sin37°=0.6,cos37°=0.8.求: