题目内容
8.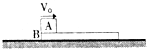 如图所示,一长为1m,质量为mB=2kg的木板B静止在水平地面上,B与地面间的动摩擦因数为μB=0.2,一质量为mA=3kg的小铁块A(可视为质点)从B的左端以V0=3m/s的初速度向右滑上木板,A、B之间动摩擦因数为μA=0.4.求:
如图所示,一长为1m,质量为mB=2kg的木板B静止在水平地面上,B与地面间的动摩擦因数为μB=0.2,一质量为mA=3kg的小铁块A(可视为质点)从B的左端以V0=3m/s的初速度向右滑上木板,A、B之间动摩擦因数为μA=0.4.求:(1)A对B的相对位移SAB
(2)最终A对地的位移SA.
分析 (1)滑块滑上木板滑块做匀减速直线运动,木板做匀加速直线运动,达到共同速度后,共同做减速运动直至停止,根据牛顿第二定律分别求出它们的加速度,求出两物体速度相同时所需的时间,从而求出小滑块相对地面的位移大小和A对B的相对位移SAB;
(2)求出共同做减速运动直至停止的位移,从而求出小滑块自滑上长板到最后静止(相对地面)的过程中运动的位移.
解答 解:对于A,它开始减速运动的加速度大小:
a1=-$\frac{{μ}_{A}{m}_{A}g}{{m}_{A}}$=-μAg=-0.4×10=-4m/s2
设B的加速度大小为a2:
a2=$\frac{{μ}_{A}mg-{μ}_{B}({m}_{A}+{m}_{B})g}{{m}_{B}}$=$\frac{0.4×3×10-0.2×(2+3)×10}{2}=1$m/s2
由于A减速,B加速,设经过时间t1二者达到共同速度,
有V0+a1t1=a2t1,
代入数据,解得:t1=0.6 s
A在这段时间内滑行的位移:
X1=V0t1+$\frac{1}{2}{a}_{1}{t}_{1}^{2}$=3×$0.6-\frac{1}{2}×4×0.{6}^{2}$=1.08m
B在这段时间内滑行的位移:
X2=$\frac{1}{2}{a}_{2}{t}_{1}^{2}=\frac{1}{2}×1×0.{6}^{2}=\frac{1}{2}×1×0.{6}^{2}=0.18$m
小滑块滑上长木板后,相对于长木板运动的总位移:
△x=X1-X2=1.08-0.18=0.9m
(2)当二者达到共同速度后,由于地面摩擦,设将一起做减速运动,共同运动时加速度加速度大小为a3,
${a}_{3}=-\frac{{μ}_{B}({m}_{A}+{m}_{B})g}{{{m}_{A}+m}_{B}}=-{μ}_{B}g=-0.2×10=-2m/{s}^{2}$
可知$|\begin{array}{l}{{a}_{3}}\\{\;}\end{array}|<|\begin{array}{l}{{a}_{1}}\\{\;}\end{array}|$,之后A与B一起做减速运动,后阶段的初速度为:
V=a2t1=1×0.6=0.6m/s
A与B一起做减速运动的位移为:
X3=$\frac{{0-V}^{2}}{2{a}_{3}}=\frac{0-0.{6}^{2}}{2×(-2)}=0.09$m
则全过程m相对于地移动的距离为:
X=X1+X3=1.08+0.09=1.17m
答:(1)小滑块A滑上长木板后,A对B的相对位移是0.9m;(2)最终A对地的位移是1.17m.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,关键理清滑块和木板的运动情况,结合牛顿第二定律和运动学公式求解.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 质量大的物体动能也大 | B. | 速度大的物体动能也大 | ||
| C. | 加速度大的物体动能也大 | D. | 物体的动能不可能小于零 |
| A. | 时间缓慢 | B. | 长度收缩 | C. | 质量变小 | D. | 时空弯曲 |
| A. | 一个力增大,合力一定增大 | B. | 两个力都增大,合力一定增大 | ||
| C. | 两个力都增大,合力可能增大 | D. | 两个力都增大,合力可能减小 |
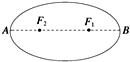 某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于( )
某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于( )| A. | F2点 | B. | A点 | C. | F1点 | D. | B点 |
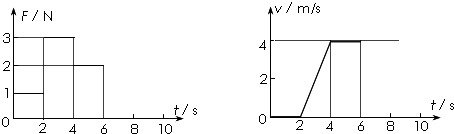
| A. | m=0.5kg,μ=0.4 | B. | m=1.5kg,μ=$\frac{2}{15}$ | C. | m=0.5kg,μ=0.2 | D. | m=1kg,μ=0.2 |
 如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.不计空气阻力.下列说法正确的是( )
如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.不计空气阻力.下列说法正确的是( )| A. | 小球从A出发到返回A的过程中,位移为零,外力做功为零 | |
| B. | 小球从A到C与从C到B的过程中,减少的动能相等 | |
| C. | 小球从A到C与从C到B的过程中,速度的变化率不相等 | |
| D. | 小球从A到C与从C到B的过程中,损失的机械能不相等 |
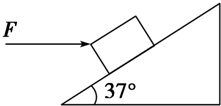 如图所示,在倾角为37°的固定斜面上放一重20N的物体,在水平方向F=10N的推力作用下处于静止状态.(已知sin37°=0.6,cos37°=0.8)求:
如图所示,在倾角为37°的固定斜面上放一重20N的物体,在水平方向F=10N的推力作用下处于静止状态.(已知sin37°=0.6,cos37°=0.8)求: 如图所示,是某兴趣小组研究平抛运动的实验装置.两个相同的弧形轨
如图所示,是某兴趣小组研究平抛运动的实验装置.两个相同的弧形轨