题目内容
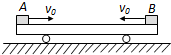 质量为M=4.0kg的平板小车静止在光滑的水平面上,如图所示,当t=0时,两个质量分别为mA=2kg、mB=1kg的小物体A、B都以大小为v0=7m/s.方向相反的水平速度,同时从小车板面上的左右两端相向滑动.直到它们在小车上停止滑动时都没有相碰,A、B与小车板面间的动摩擦因数均为μ=0.2,取g=10m/s2,求:
质量为M=4.0kg的平板小车静止在光滑的水平面上,如图所示,当t=0时,两个质量分别为mA=2kg、mB=1kg的小物体A、B都以大小为v0=7m/s.方向相反的水平速度,同时从小车板面上的左右两端相向滑动.直到它们在小车上停止滑动时都没有相碰,A、B与小车板面间的动摩擦因数均为μ=0.2,取g=10m/s2,求:(1)A、B在车上都停止滑动时整体共同的速度
(2)A、B在小车上滑动过程中,系统损失的机械能
(3)从A、B开始滑动到都停止滑动一共经历了多长时间.
分析:1、全过程,对系统,由动量守恒列出等式求解.
2、全过程,对系统,由能量守恒求解
3、对滑块从开始滑动到相对小车停止滑动的过程,根据动量定理求解.
2、全过程,对系统,由能量守恒求解
3、对滑块从开始滑动到相对小车停止滑动的过程,根据动量定理求解.
解答:解:(1)全过程,对系统,由动量守恒,令向右为正:
mAv0-mBv0=(M+mA+mB)v′
整体共同的速度为v′=1m/s
(2)全过程,对系统,由能量守恒得
△E机=
mA
+
mB
-
(M+mA+mB)v′2
所以,系统损失的机械能:
△E机=70J
(3)根据动量定理得:
F合t=△p=m△v
对滑块从开始滑动到相对小车停止滑动的过程有:
mgμ△t=m△v
所以滑块在小车上的滑动时间:△t=
由于B滑块的速度变化△v比A滑块大,所以相对小车的滑行时间长
所以一共经历的滑行时间为:△t=△tB=
=4s
答:(1)A、B在车上都停止滑动时整体共同的速度是1m/s
(2)A、B在小车上滑动过程中,系统损失的机械能是70J
(3)从A、B开始滑动到都停止滑动一共经历了4s.
mAv0-mBv0=(M+mA+mB)v′
整体共同的速度为v′=1m/s
(2)全过程,对系统,由能量守恒得
△E机=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
所以,系统损失的机械能:
△E机=70J
(3)根据动量定理得:
F合t=△p=m△v
对滑块从开始滑动到相对小车停止滑动的过程有:
mgμ△t=m△v
所以滑块在小车上的滑动时间:△t=
| △v |
| gμ |
由于B滑块的速度变化△v比A滑块大,所以相对小车的滑行时间长
所以一共经历的滑行时间为:△t=△tB=
| △vB |
| gμ |
答:(1)A、B在车上都停止滑动时整体共同的速度是1m/s
(2)A、B在小车上滑动过程中,系统损失的机械能是70J
(3)从A、B开始滑动到都停止滑动一共经历了4s.
点评:对于物块在小车上,往往动量守恒,有时还用到能量守恒求解.

练习册系列答案
相关题目
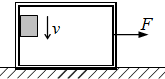 如图所示,质量为M=4.0kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右运动,铁箱与水平面间的动摩擦因数为μ1=0.20.这时铁箱内一个质量为m=1.0kg的木块恰好能沿箱的后壁向下匀速下滑,木块与铁箱间的动摩擦因数为μ2=0.50.求水平拉力F的大小.(取g=10m/s2)
如图所示,质量为M=4.0kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右运动,铁箱与水平面间的动摩擦因数为μ1=0.20.这时铁箱内一个质量为m=1.0kg的木块恰好能沿箱的后壁向下匀速下滑,木块与铁箱间的动摩擦因数为μ2=0.50.求水平拉力F的大小.(取g=10m/s2)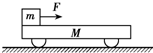 如图所示,有一长度为x=1.0m、质量为M=10Kg的平板小车,静止在光滑的水平面上,在小车的左端放置一质量为m=4.0Kg的小物块,物块与小车之间的动摩擦因数为μ=0.25,要使物块在t=2.0s内运动到小车的右端,则施加在小物块上的水平向右的拉力大小应为多少?(g=10m/s2)
如图所示,有一长度为x=1.0m、质量为M=10Kg的平板小车,静止在光滑的水平面上,在小车的左端放置一质量为m=4.0Kg的小物块,物块与小车之间的动摩擦因数为μ=0.25,要使物块在t=2.0s内运动到小车的右端,则施加在小物块上的水平向右的拉力大小应为多少?(g=10m/s2)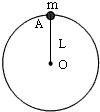 如图所示,长度为L=1.00m的轻质细杆OA,A端有一质量为m=4.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是v=2.0m/s,则细杆OA受到(g取10m/s2)( )
如图所示,长度为L=1.00m的轻质细杆OA,A端有一质量为m=4.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是v=2.0m/s,则细杆OA受到(g取10m/s2)( ) 如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2