Question

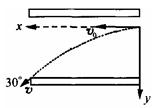
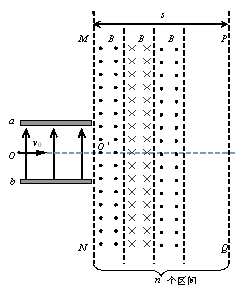
（16分）如图所示，两水平放置的平行金属板a、b，板长L＝0.2 m，板间距d＝0.2 m．两金属板间加可调控的电压U，且保证a板带负电，b板带正电， 忽略电场的边缘效应．在金属板右侧有一磁场区域，其左右总宽度s＝0.4 m，上下范围足够大，磁场边界MN和PQ均与金属板垂直，磁场区域被等宽地划分为n（正整数）个竖直区间，磁感应强度大小均为B＝5×10^-3T，方向从左向右为垂直纸面向外、向内、向外……．在极板左端有一粒子源，不断地向右沿着与两板等距的水平线OO′发射比荷＝1×10⁸ C/kg、初速度为v₀＝2×10⁵ m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用．
（1）当取U何值时，带电粒子射出电场时的速度偏向角最大；
（2）若n=1，即只有一个磁场区间，其方向垂直纸面向外，则当电压由0连续增大到U过程中带电粒子射出磁场时与边界PQ相交的区域的宽度；
（3）若n趋向无穷大，则偏离电场的带电粒子在磁场中运动的时间t为多少？

Answer 1

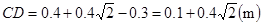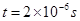
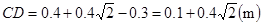（1）400V （2）（3）

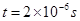
试题分析：（1）（4分）设速度偏向角为（，则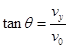，显然当v_y最大时，（ 最大。
当粒子恰好从极板右边缘出射时，速度偏向角最大。          （1分）
竖直方程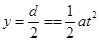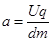：，；                       （1分）
水平方程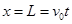：                                    （1分）
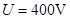解得：                （1分）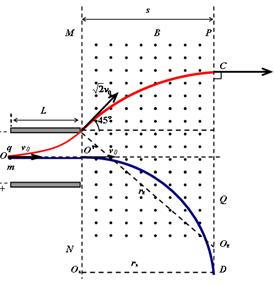

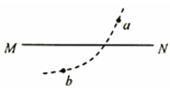
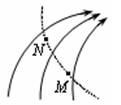
（2）（7分）由几何关系知，逐渐增大U_ba，速度偏向角变大，磁偏转半径变大，与PQ交点逐渐上移。             
当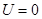时，交点位置最低（如图中D点）：                         
由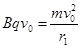得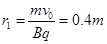，    （1分）
此时交点D位于OO′正下方0.4m处。    （1分）
当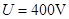时，交点位置最高（如图中C点）：
由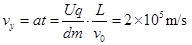，       （1分）
得,   （1分）
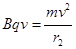由，得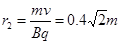，   （1分）
由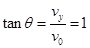，得入射方向为与水平方向成45°角
由几何关系得，此时交点位于OO′正上方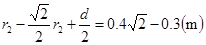处。 （1分）
所以交点范围宽度为 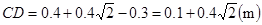            （1分）
（3）（5分）考虑粒子以一般情况入射到磁场，速度为v，偏向角为（，当n趋于无穷大时，运动轨迹趋于一条沿入射速度方向的直线（渐近线）。                     （1分）
又因为速度大小不变，因此磁场中运动可以等效视为匀速直线运动。       （1分）

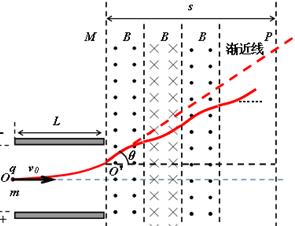
轨迹长度为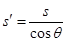，运动速率为 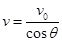                （1分）
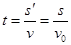时间                                            （1分）
代入数据解得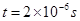：                                 （1分）
【评分参考】：第（3）问中：①若直接写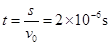，得2分；②如果学生用微元过程证明，并得出总时间为定值，也可得过程分2~3分，结果对再给2分