题目内容
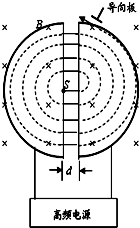 如图为回旋加速器示意图,其中置于高真空中的金属D形盒的半径为R,两盒间距为d(d<<R),在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示.质子质量为m,电荷量为q.设质子从粒子源S进入加速电场时的初速度不计,加速质子时的电压恒为U,质子在电场中运动时,不考虑磁场的影响.求:
如图为回旋加速器示意图,其中置于高真空中的金属D形盒的半径为R,两盒间距为d(d<<R),在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示.质子质量为m,电荷量为q.设质子从粒子源S进入加速电场时的初速度不计,加速质子时的电压恒为U,质子在电场中运动时,不考虑磁场的影响.求:(1)此加速器所需的高频电源频率f;
(2)质子能达到的最大速度;
(3)质子在电场中运动的时间和在D形盒中回旋的时间,并说明质子在电场中加速的时间可忽略不计.
分析:(1)根据质子做匀速圆周运动的周期公式,即可求解;
(2)根据运动半径等于R,结合牛顿第二定律与向心力,即可求解;
(3)根据加速后最大动能,结合加速次数,从而可确定加速与回旋时间.
(2)根据运动半径等于R,结合牛顿第二定律与向心力,即可求解;
(3)根据加速后最大动能,结合加速次数,从而可确定加速与回旋时间.
解答:解:(1)质子的回旋周期为:T=
=
①
高频电源的频率为:f=
=
②
(2)当回旋半径r=R时,质子的速度最大
qvmB=m
得vm=
③
(3)质子加速后的最大动能为:Ek=
m
=
④
设质子在电场中加速的次数为n,则:n=
⑤
在电场中加速的总时间为:t1=
=
⑥
由③④⑤⑥得t1=
(或t1=
)
在D形盒中回旋的时间为t2=n
⑦
由①④⑤得t2=
=
,
由于d<<R,则说明质子在电场中加速的时间可忽略不计.
答:(1)此加速器所需的高频电源频率f=
;
(2)质子能达到的最大速度得vm=
;
(3)质子在电场中运动的时间得t1=
和在D形盒中回旋的时间得t2=
,由于d<<R,则质子在电场中加速的时间可忽略不计.
| 2πR |
| v |
| 2πm |
| qB |
高频电源的频率为:f=
| 1 |
| T |
| qB |
| 2πm |
(2)当回旋半径r=R时,质子的速度最大
qvmB=m
| ||
| R |
得vm=
| qBR |
| m |
(3)质子加速后的最大动能为:Ek=
| 1 |
| 2 |
| v | 2 m |
| q2B2R2 |
| 2m |
设质子在电场中加速的次数为n,则:n=
| Ek |
| qU |
在电场中加速的总时间为:t1=
| nd | ||
|
| 2nd |
| vm |
由③④⑤⑥得t1=
| BdR |
| U |
| vm |
| a |
在D形盒中回旋的时间为t2=n
| T |
| 2 |
由①④⑤得t2=
| πBR2 |
| 2U |
| t1 |
| t2 |
| 2d |
| πR |
由于d<<R,则说明质子在电场中加速的时间可忽略不计.
答:(1)此加速器所需的高频电源频率f=
| qB |
| 2πm |
(2)质子能达到的最大速度得vm=
| qBR |
| m |
(3)质子在电场中运动的时间得t1=
| BdR |
| U |
| πBR2 |
| 2U |
点评:考查粒子做匀速圆周的周期公式与半径公式的应用,掌握牛顿第二定律,注意区别求加速时间与回旋时间的不同.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
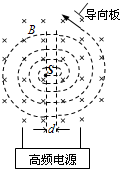 正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.
正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.


