��Ŀ����
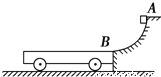
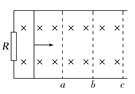
����Ŀ����ͼ��ʾ��ˮƽ�⻬��ƽ�н������죬��������R����������ǿ�ų�B��ֱ���·ֲ��ڵ������ڵĿռ��ڣ�����һ���Ľ������ڴ�ֱ����ķ��������ڵ���������ʹ����һ���ij��ٶ������˶�������ͨ��λ��aʱ����Ϊva��ͨ��λ��bʱ����Ϊvb����λ��cʱ���պþ�ֹ���赼�������ĵ����������a��b��b��c�ļ����ȣ��Խ���������a��b��b��c�����������У���·�в����ĵ���Eab��Ebc֮��Ϊ���
���𰸡�![]()
�������������������˶�ʱ���и�Ÿ��ߣ���·�в�����Ӧ�������������ֶ����֪�����������ܰ������谭���˶��������������a��b�����У�����ƽ��������ΪF1��ʱ��Ϊt1����b��c�����У�����ƽ��������ΪF2��ʱ��Ϊt2������֮�����Ϊd��
��![]()
ͬ��![]()
���ݶ�����������F1t1��mvb��mva����![]() ��
��
��F2t2��0��rnvb����![]() ��
��
����ΪLab��Lbc ��
���٢ڢ�ʽ��mva��mvb��mvb
����va��2vb
���������غ���![]()
![]()
��

��ϰ��ϵ�д�
�����Ŀ