题目内容
 如图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度B=0.10T,磁场区域半径r=
如图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度B=0.10T,磁场区域半径r=| 2 |
| 3 |
| 3 |
(1)该离子通过两磁场区域所用的时间.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为多大?(侧移距离指垂直初速度方向上移动的距离)
分析:粒子从A点进入匀强磁场后,由洛伦兹力提供向心力,做匀速圆周运动,根据牛顿第二定律求出轨迹半径,得出轨迹的圆心角,由运动时间与周期的关系求出粒子从A到C的时间.粒子穿越右侧磁场的时间与穿越左侧磁场的时间相等,再求解总时间.
根据运动轨迹与几何关系可确定离子离开右侧区域的出射点偏离最初入射方向的侧移距离.
根据运动轨迹与几何关系可确定离子离开右侧区域的出射点偏离最初入射方向的侧移距离.
解答: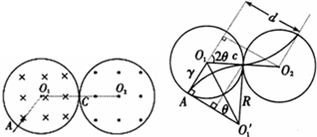 解:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,
解:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,
如右图,设轨迹半径为R,圆周运动的周期为T,
由牛顿第二定律得,Bqv=m
,又因:T=
,联立可得,R=
T=
解得:R=2m,
由轨迹图知,tanθ=
=
则θ=30°
所以全段轨迹运动时间为:t=2×
×2θ=
联立可解得,t=4.19×10-6s
(2)在图中过O2向AO1作垂线,联立轨迹对称关系,侧移总距离为d=2rsin2θ=2m
答:(1)该离子通过两磁场区域所用的时间4.19×10-6s.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为2m.
 解:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,
解:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,如右图,设轨迹半径为R,圆周运动的周期为T,
由牛顿第二定律得,Bqv=m
| v2 |
| R |
| 2πR |
| v |
| mv |
| Bq |
| 2πR |
| Bq |
解得:R=2m,
由轨迹图知,tanθ=
| r |
| R |
| ||
| 3 |
所以全段轨迹运动时间为:t=2×
| T |
| 360° |
| T |
| 3 |
联立可解得,t=4.19×10-6s
(2)在图中过O2向AO1作垂线,联立轨迹对称关系,侧移总距离为d=2rsin2θ=2m
答:(1)该离子通过两磁场区域所用的时间4.19×10-6s.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为2m.
点评:本题是有界磁场问题,关键是画出粒子的运动轨迹,运用几何知识求解半径.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
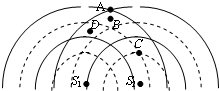 如图所示,S1、S2是两个频率相同的波源,它们发出的两列简谐横波在空间相遇,图中虚线和实线分别代表某时刻这两列波的波谷和波峰,则下列说法中正确的是( )
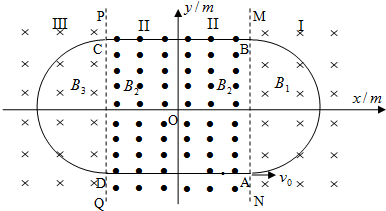
如图所示,S1、S2是两个频率相同的波源,它们发出的两列简谐横波在空间相遇,图中虚线和实线分别代表某时刻这两列波的波谷和波峰,则下列说法中正确的是( ) (2009?日照一模)某同学设想用带电粒子的运动轨迹做出“0”、“8”字样,首先,如图甲所示,在真空空间的竖直平面内建立.roy坐标系,在y1=0.1m和y2=一0.1m处有两个与z轴平行的水平界面PQ和MN把空间分成I、Ⅱ、Ⅲ三个区域,在三个区域中分别存在匀强磁场B1、B2、B3其大小满足B=2=B1=2B3=0.02T,方向如图甲所示.在Ⅱ区域中的y轴左右两侧还分别存在匀强电场E1、E2(图中未画出),忽略所有电、磁场的边缘效应.ABCD是以坐标原点.为中心对称的正方形,其边长L=0.2m.现在界面PQ上的A处沿y轴正方向发射一比荷
(2009?日照一模)某同学设想用带电粒子的运动轨迹做出“0”、“8”字样,首先,如图甲所示,在真空空间的竖直平面内建立.roy坐标系,在y1=0.1m和y2=一0.1m处有两个与z轴平行的水平界面PQ和MN把空间分成I、Ⅱ、Ⅲ三个区域,在三个区域中分别存在匀强磁场B1、B2、B3其大小满足B=2=B1=2B3=0.02T,方向如图甲所示.在Ⅱ区域中的y轴左右两侧还分别存在匀强电场E1、E2(图中未画出),忽略所有电、磁场的边缘效应.ABCD是以坐标原点.为中心对称的正方形,其边长L=0.2m.现在界面PQ上的A处沿y轴正方向发射一比荷