题目内容
8. 如图,竖直平面内的轨道I和II都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球,分别沿I和II推至最高点A,所需时间分别为t1、t2;动能增量分别为△Ek1、△Ek2,假定球在经过轨道转折点前后速度大小不变,且球与I.II轨道间的动摩擦因数相等,则( )
如图,竖直平面内的轨道I和II都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球,分别沿I和II推至最高点A,所需时间分别为t1、t2;动能增量分别为△Ek1、△Ek2,假定球在经过轨道转折点前后速度大小不变,且球与I.II轨道间的动摩擦因数相等,则( )| A. | △Ek1>△Ek2t1>t2 | B. | △Ek1=△Ek2 t1>t2 | ||
| C. | △Ek1>△Ek2 t1<t2 | D. | △Ek1=△Ek2t1<t2 |
分析 根据动能定理比较动能的增加量;通过速度时间图线,抓住路程相等,结合加速度不同,比较运动时间的长短.
解答 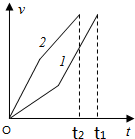 解:设任一斜面的倾角为θ,斜面的长度为s,则物体在该斜面上下滑时摩擦力做功为 Wf=-μmgcosθ•s=-μmgx,x是斜面底边的长度,可知小球沿两轨道运动时,摩擦力做功相等,根据动能定理得:
解:设任一斜面的倾角为θ,斜面的长度为s,则物体在该斜面上下滑时摩擦力做功为 Wf=-μmgcosθ•s=-μmgx,x是斜面底边的长度,可知小球沿两轨道运动时,摩擦力做功相等,根据动能定理得:
WF-mgh-Wf=△Ek,
知两次情况拉力做功相等,摩擦力做功相等,重力做功相等,则动能的变化量相等.即有△Ek1=△Ek2.
作出在两个轨道上运动的速度时间图线如图所示,由于路程相等,则图线与时间轴围成的面积相等,由图可知,t1>t2.故B正确,A、C、D错误.
故选:B
点评 本题考查了动能定理与运动学的综合,通过动能定理比较动能变化量的关系,难点在于通过速度时间图线比较运动的时间,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
15.关于速度和加速度的关系,下列说法正确的有( )
| A. | 加速度越大,速度越大 | |
| B. | 速度变化量越大,加速度也越大 | |
| C. | 加速度增大,速度可以减小 | |
| D. | 物体的速度变化越快,则加速度越大 |
16. 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示,设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示,设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示,设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示,设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )| A. | x2=$\frac{5}{2}$x1 v2=2v1 | B. | x2=$\frac{7}{2}$x1 v2=$\frac{3}{2}$v1 | ||
| C. | x2=$\frac{7}{2}$x1 W2=$\frac{5}{4}$W1 | D. | v2=2v1 W2=$\frac{5}{2}$W1 |
17. 如图所示电路中,电源电动势E恒定,内阻r=1Ω,定值电阻R3=5Ω,R2=5Ω,电容器电容C恒定,当开关K1断开与闭合时,ab段电路消耗的电功率相等.开关K1断开时,单刀双掷开关K2接1时电容器电量为Q1,接2时电量Q2.则以下说法中不正确的是( )
如图所示电路中,电源电动势E恒定,内阻r=1Ω,定值电阻R3=5Ω,R2=5Ω,电容器电容C恒定,当开关K1断开与闭合时,ab段电路消耗的电功率相等.开关K1断开时,单刀双掷开关K2接1时电容器电量为Q1,接2时电量Q2.则以下说法中不正确的是( )
 如图所示电路中,电源电动势E恒定,内阻r=1Ω,定值电阻R3=5Ω,R2=5Ω,电容器电容C恒定,当开关K1断开与闭合时,ab段电路消耗的电功率相等.开关K1断开时,单刀双掷开关K2接1时电容器电量为Q1,接2时电量Q2.则以下说法中不正确的是( )
如图所示电路中,电源电动势E恒定,内阻r=1Ω,定值电阻R3=5Ω,R2=5Ω,电容器电容C恒定,当开关K1断开与闭合时,ab段电路消耗的电功率相等.开关K1断开时,单刀双掷开关K2接1时电容器电量为Q1,接2时电量Q2.则以下说法中不正确的是( )| A. | 电阻R1可能为3Ω | |
| B. | K1断开时电压表的示数一定小于K1闭合时的示数 | |
| C. | K1断开时,K2从1变为2时,电容器所带电量变化量△Q=2.8Q1 | |
| D. | K1断开与闭合时,电压表的示数变化量大小与电流表的示数变化量大小之比等于5Ω |
 在如图所示电路,电压表和电流表均为理想电表,固定电阻R=90Ω,R0是可变电阻,可调的最大阻值为400Ω,当开关S断开时,电压表的读数为5V;当开关S闭合,调可变电阻,使电压表的读数为4.7V,电流表的读数为0.03A.
在如图所示电路,电压表和电流表均为理想电表,固定电阻R=90Ω,R0是可变电阻,可调的最大阻值为400Ω,当开关S断开时,电压表的读数为5V;当开关S闭合,调可变电阻,使电压表的读数为4.7V,电流表的读数为0.03A.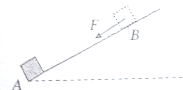 如图所示,斜面倾角θ=30°的光滑斜面上,高h=1m的位置B点,放置一质量为m=1kg的物体.(g取10m/s2)
如图所示,斜面倾角θ=30°的光滑斜面上,高h=1m的位置B点,放置一质量为m=1kg的物体.(g取10m/s2)