题目内容
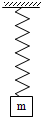 有一轻弹簧,原长L0=0.50m,劲度系数k=100N/m,上端固定.在其下端挂一质量m=1.0kg的铁块后,再将铁块竖直向下拉,使弹簧长度变为L1=0.90m.然后由静止释放铁块,则铁块在竖直方向上做简谐运动.如果知道铁块在平衡位置时的弹性势能EP1=0.50J,经过平衡位置时速度vm=3.0m/s.(g=10m/s2 )
有一轻弹簧,原长L0=0.50m,劲度系数k=100N/m,上端固定.在其下端挂一质量m=1.0kg的铁块后,再将铁块竖直向下拉,使弹簧长度变为L1=0.90m.然后由静止释放铁块,则铁块在竖直方向上做简谐运动.如果知道铁块在平衡位置时的弹性势能EP1=0.50J,经过平衡位置时速度vm=3.0m/s.(g=10m/s2 )求:(1)铁块在做简谐振动时的振幅A;
(2)铁块在振动过程到达最高点时弹簧的弹性势能EP2.
分析:(1)设铁块处于平衡位置O时,弹簧的长度为L2,此时弹簧弹力等于重力,根据平衡条件求出L2,铁块作简谐运动,其振幅为A=L1-L2;
(2)得铁块到达最高点时动能为零,根据系统机械能守恒列式即可求解.
(2)得铁块到达最高点时动能为零,根据系统机械能守恒列式即可求解.
解答:解:(1)设铁块处于平衡位置O时,弹簧的长度为L2,则L2=L0+
=0.50+
m=0.60m
铁块作简谐运动,其振幅为A=L1-L2=0.9m-0.6m=0.30m
(2)由机械能守恒定律,得EP2=
m
-mgA+EP1
代入已知数值,得铁块到达最高点时弹簧的弹性势能为
EP2=
×1×3.02J-1.0×10×0.30J+0.5 J=2.0 J
答:(1)铁块在做简谐振动时的振幅A为0.30m;
(2)铁块在振动过程到达最高点时弹簧的弹性势能为2.0J.
| mg |
| k |
| 10 |
| 100 |
铁块作简谐运动,其振幅为A=L1-L2=0.9m-0.6m=0.30m
(2)由机械能守恒定律,得EP2=
| 1 |
| 2 |
| v | 2 m |
代入已知数值,得铁块到达最高点时弹簧的弹性势能为
EP2=
| 1 |
| 2 |
答:(1)铁块在做简谐振动时的振幅A为0.30m;
(2)铁块在振动过程到达最高点时弹簧的弹性势能为2.0J.
点评:本题主要考查了机械能守恒定律和胡克定律的直接应用,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

