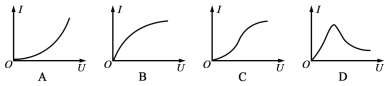题目内容
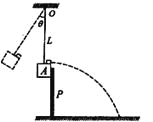
【题目】如图所示,半径为R的四分之一圆轨道OA与水平桌面AB相切,圆轨道光滑绝缘。一质量为m、电荷量+q的滑块从距水平桌面高为![]() 处的圆弧面上静止滑下,最后停在C点。在绝缘桌面MN间存在垂直于水平面的匀强电场。已知滑块经过AM,NC时间相同,AM=MN=3NC=3
处的圆弧面上静止滑下,最后停在C点。在绝缘桌面MN间存在垂直于水平面的匀强电场。已知滑块经过AM,NC时间相同,AM=MN=3NC=3![]() ,重力加速度为g,滑块与桌面间摩擦因数为
,重力加速度为g,滑块与桌面间摩擦因数为![]() 。试求:
。试求:
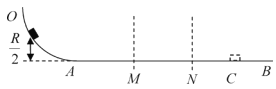
(1)滑块刚滑到圆弧末端A点时对轨道压力
(2)判断在MN中物体的运动情况,并求出匀强电场电场强度
(3)若仅改变电场区域MN与圆轨道间的距离,并耍求滑块能穿过电场区域,求滑块在桌面滑行的最短时间。
【答案】(1)2mg,方向竖直向下。(2)![]() ,方向垂直水平面向上(3)
,方向垂直水平面向上(3)![]()
【解析】试题分析:
(1)滑块从弧面上滑下时机械能守恒,固有![]()
而在A点:![]()
联立解得:FN=2mg
根据牛顿第三定律,滑块在A点对轨道的压力为2mg,方向竖直向下。
(2)滑块在AM、NC间水平方向上只受摩擦力,做匀减速运动,加速度大小为![]()
假设滑块在M点速度为vM,在N点速度为vN 则有:![]()
![]() ,
,![]()
联立各式可得:![]()
故在MN间滑块做匀速运动,故有Eq="mg"
得:![]() ,方向垂直水平面向上.
,方向垂直水平面向上.
(3)无论电场位置如何,滑块做减速运动的时间不会变化,要求时间最短则要求在电场中的时间最短即可,即要求在电场中速度最大,当AM重合即可满足要求.
减速的时间![]()
电场中的时间![]()
故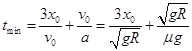

 备战中考寒假系列答案
备战中考寒假系列答案【题目】如图为“探究物体的加速度与质量和受力的关系”的实验装置。沙和沙桶的质量为m,小车和砝码的质量为M。实验中将沙和沙桶的重力作为细线对小车的拉力。
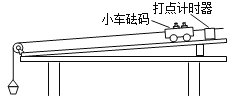
(1)实验前,在进行平衡摩擦力的操作时,下列注意事项正确的是
A.应该让小车连接纸带并穿过打点计时器 |
B.必须让小车连接沙桶 |
C.纸带和沙桶都应连接 |
D.纸带和沙桶都不能连接 |
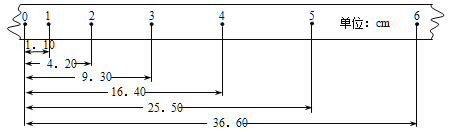
(2)现保持沙和沙桶的总质量m不变,改变小车和砝码的总质量M,探究加速度和质量的关系。如图是某次实验中打出的一条纸带,交变电流的频率为50Hz,每隔4个点选一个计数点,则小车的加速度为____m/s2(保留两位有效数字)。通过实验得到多组加速度a、质量M的数据,为了方便准确地研究二者关系,一般选用纵坐标为加速度a,则横坐标为__ __(填M或![]() )。
)。