题目内容
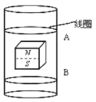
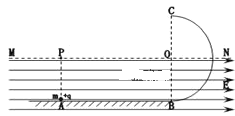
【题目】如图所示,光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接.在过圆心O的水平界面MN的下方分布有水平向右的匀强电场.现有一质量为m,电量为+q的小球从水平轨道上A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,如图.小球可视为质点,小球运动到C点之前电量保持不变,经过C点后电量立即变为零.已知A、B间距离为2R,重力加速度为g.在上述运动过程中,求:
(1)小球离开C点时的速率;
(2)电场强度E的大小;
(3)在圆轨道上什么位置小球对轨道的压力最大,并求出最大压力.
【答案】(1)![]() (2)
(2)![]() (3)(2+3
(3)(2+3![]() )mg
)mg
【解析】
(1)小球离开C点做平抛运动,根据
![]()
得
![]()
则小球在C处的速度
![]()
(2)设电场强度为E,小球从A到C由动能定理得,
![]()
解得
![]()
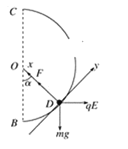
(3)设小球运动到圆轨道D点时速度最大,设最大速度为v,此时OD与竖直线OB夹角设为α,小球从A点运动到D点的过程,根据动能定理知
![]()
即
![]()
根据数学知识可知,当α=45°时动能最大,由此可得
![]()
故小球在D点时对圆轨道的压力最大,设此压力大小为F,由牛顿第三定律可知小球在D点受到的轨道的弹力大小也为F,在D点对小球进行受力分析,并建立如图所示坐标系,
由牛顿第二定律知
![]()
解得
![]()

练习册系列答案
相关题目