题目内容
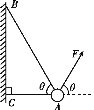
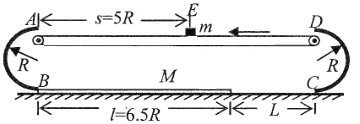
【题目】如图所示，以A、B 和C、D 为断点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑的地面上，左端紧靠B 点，上表面所在平面与两半圆分别相切于B、C 两点，一物块（视为质点）被轻放在水平匀速运动的传送带上E 点，运动到A 点时刚好与传送带速度相同，然后经A 点沿半圆轨道滑下，且在B 点对轨道的压力大小为10mg，再经B 点滑上滑板，滑板运动到C 点时被牢固粘连。物块可视为质点，质量为m，滑板质量为M=2m，两半圆半径均为R，板长l=6.5R,板右端到C 点的距离为L=2.5R，E 点距A 点的距离s=5R，物块与传送带、物块与滑板间的动摩擦因数相同，重力加速度为g。求：
(1)物块滑到B点的速度大小.
(2)物块与传送带、物块与滑板间的动摩擦因数.
(3)物块与滑板间因摩擦而产生的总热量
【答案】（1）
（2）0.5（3）
【解析】
在B点，由轨道的支持力和重力的合力提供向心力，根据向心力公式求解；从E到B的过程中，根据动能定理求解；滑块滑上木板后做匀减速直线运动，木板做匀加速直线运动，根据牛顿第二定律求解加速度，根据运动学基本公式判断速度相当时的位置关系，再根据摩擦力做功公式结合能量守恒求解。
（1）设物块运动到B的速度为vB，由牛顿第二定律得：
解得：
（2）从E到B由动能定理得
解得：
=0.5
（3）物块从B点滑上滑板时至物块与滑板共速，根据动量守恒：
解得：
对m，根据动能定理：
解得：x1=8R
对M，根据动能定理：
解得：x2=2R
因为：
<6.5R
可知物块与滑板达到共同速度时，物块未离开滑板：
物块与木板此后以共同速度匀速运动至C点，滑板不再运动，物块在滑板上继续往前运动
对m，根据动能定理：
解得：
由上可知
可知物块不能到达与圆心同一高度的点，将会沿圆轨道滑回来，由能量守恒可得：
总热量：Q=Q1+Q2+Q3=3.5mgR
