题目内容
11.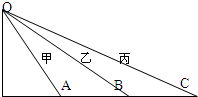 如图所示,三个光滑斜轨道OA、OB、OC,它们的倾角依次是60°、45°、30°,这些轨道交于O点,现有三个小物体甲、乙、丙,分别沿这三个轨道同时从O点由静止自由下滑,物体分别滑到斜面底端点A、B、C的先后顺序是( )
如图所示,三个光滑斜轨道OA、OB、OC,它们的倾角依次是60°、45°、30°,这些轨道交于O点,现有三个小物体甲、乙、丙,分别沿这三个轨道同时从O点由静止自由下滑,物体分别滑到斜面底端点A、B、C的先后顺序是( )| A. | 甲最先,乙稍后,丙最后 | B. | 甲、乙、丙同时到达 | ||
| C. | 乙最先,然后甲和丙同时到达 | D. | 丙最先,乙稍后,甲最后 |
分析 根据牛顿第二定律求出在光滑斜面上下滑的加速度,根据匀变速直线运动的位移时间公式求出运动的时间,根据数学的三角函数求出时间的最小值
解答 解:设斜面的倾角为θ,则下滑的加速度$\frac{mgsinθ}{m}=gsinθ$,下滑的位移x=$\frac{h}{sinθ}$,根据x=$\frac{1}{2}a{t}^{2}$得,$t=\sqrt{\frac{2x}{a}}=\sqrt{\frac{2h}{gsi{n}^{2}θ}}$
故倾角越大的下落时间越短,故甲最先,乙稍后,丙最后,故A正确
故选:A
点评 本题综合运用了牛顿第二定律和运动学知识,知道加速度是联系前后的桥梁,通过加速度可以根据力求运动

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
6.某驾驶员手册规定具有良好刹车性能的汽车在以90km/h的速率行驶时,可以在80m的距离内被刹住;在以54km/h的速率行驶时,可以在33m的距离内被刹住.假设对于这两种速率,驾驶员所允许的反应时间(在反应时间内驾驶员来不及使用刹车,车速不变)与刹车的加速度都相同,则允许驾驶员的反应时间约为( )
| A. | 0.2s | B. | 0.4s | C. | 0.5s | D. | 0.7s |
16.在验证平行四边形定则实验中,橡皮条的一端固定在木板上,用两个测力计把橡皮条的另一端拉到同一确定的O点.以下操作中错误的有( )(不定项选择)
| A. | 同一实验过程中,O点位置可以改变 | |
| B. | 实验中,测力计必须保持与木板平行,读数时视线要正对测力计刻度 | |
| C. | 实验中,先将一个测力计沿某一方向拉到最大量程,然后只需调整另一测力计的大小和方向,把橡皮条另一端拉到O点 | |
| D. | 实验中,把橡皮条的另一端拉到O点时,两个测力计之间的夹角取90°,以便算出合力的大小 | |
| E. | 实验中,只需记录下两个测力计拉和一个测力计单独拉时的力的大小即可 |
3.小球做匀速圆周运动,半径R=0.1m,向心加速度的大小为a=0.4m/s2,则下列说法中正确的是( )
| A. | 小球做匀速圆周运动,故小球处于平衡状态,速度不变 | |
| B. | 小球运动的角速度为2rad/s | |
| C. | 小球一定受到向心力作用 | |
| D. | 小球运动的线速度大小为0.04 m/s |
20.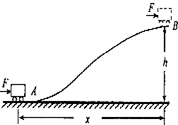 如图所示,质量为m的小车在水平恒力F的推动下,从山坡(粗糙)底部A处由静止运动至高为h的山坡顶部B处,获得的速度为v,A、B之间的水平距离为x,重力加速度为g.下列说法正确的是( )
如图所示,质量为m的小车在水平恒力F的推动下,从山坡(粗糙)底部A处由静止运动至高为h的山坡顶部B处,获得的速度为v,A、B之间的水平距离为x,重力加速度为g.下列说法正确的是( )
 如图所示,质量为m的小车在水平恒力F的推动下,从山坡(粗糙)底部A处由静止运动至高为h的山坡顶部B处,获得的速度为v,A、B之间的水平距离为x,重力加速度为g.下列说法正确的是( )
如图所示,质量为m的小车在水平恒力F的推动下,从山坡(粗糙)底部A处由静止运动至高为h的山坡顶部B处,获得的速度为v,A、B之间的水平距离为x,重力加速度为g.下列说法正确的是( )| A. | 小车克服重力做的功是-mgh | |
| B. | 合外力对小车做的功是$\frac{1}{2}$mv2+mgh | |
| C. | 阻力对小车做的功是Fx-mgh-$\frac{1}{2}$mv2 | |
| D. | 推力对小车做的功是$\frac{1}{2}$mv2+mgh-W阻 |
1.甲物体的重量是乙物体重量的2倍,甲从H高处自由落下,乙从2H高处同时自由落下,以下说法正确的为(不计空气阻力,甲、乙均未落地)( )
| A. | 下落1s时,它们的位移相等 | |
| B. | 下落过程中甲的加速度比乙的大 | |
| C. | 下落1m时,它们的速度相等 | |
| D. | 两物体下落过程中,同一时刻甲的速率比乙大 |
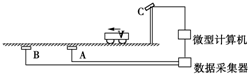 在上海的高架道路上,一般限速80km/h,为监控车辆是否超速,设置了一些“电子警察”系统,其工作原理如图所示:路面下相隔L埋设两个传感器线圈A和B,当有车辆经过线圈正上方时,传感器能向数据采集器发出一个电信号;若有一辆汽车(在本题中可看作质点)匀速经过该路段,两传感器先后向数据采集器发送信号,时间间隔为△t,经微型计算机处理后得出该车的速度,若超速,则计算机将指令架设在路面上方的照相机C对汽车拍照,留下违章证据.根据以上信息,回答下列问题:
在上海的高架道路上,一般限速80km/h,为监控车辆是否超速,设置了一些“电子警察”系统,其工作原理如图所示:路面下相隔L埋设两个传感器线圈A和B,当有车辆经过线圈正上方时,传感器能向数据采集器发出一个电信号;若有一辆汽车(在本题中可看作质点)匀速经过该路段,两传感器先后向数据采集器发送信号,时间间隔为△t,经微型计算机处理后得出该车的速度,若超速,则计算机将指令架设在路面上方的照相机C对汽车拍照,留下违章证据.根据以上信息,回答下列问题: 如图所示,在无穷大的光滑水平面上有两个物块A、B,质量分别为M、m(M>m),物块A右端拴接轻弹簧l.现用物块B将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为E0时,释放物块B.物块B被弹簧2弹开后,碰到弹簧l(不粘连),由于M比m大,物块B被反弹,以后B将在两弹簧之间往复运动.则从释放物块B开始,在以后整个运动过程中:
如图所示,在无穷大的光滑水平面上有两个物块A、B,质量分别为M、m(M>m),物块A右端拴接轻弹簧l.现用物块B将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为E0时,释放物块B.物块B被弹簧2弹开后,碰到弹簧l(不粘连),由于M比m大,物块B被反弹,以后B将在两弹簧之间往复运动.则从释放物块B开始,在以后整个运动过程中: