题目内容
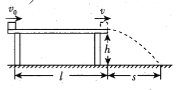
【题目】如图所示，位置O为轻质弹簧竖直固定时的原长位置，把一质量为m的薄板放在弹簧上端，静止后弹簧恰能被压缩到B位置，距离位置O为x。从距离位置O为2x的A位置由静止释放一质量为m的物块，与薄板碰撞后马上随薄板一起向下运动，最后弹簧上端随薄板和物块刚好能返回到位置O，重力加速度为g，求
（1）物块与薄板碰撞前的速度。
（2）弹簧被压缩到位置B时的弹性势能。
【答案】（1）
（2）
【解析】试题分析：根据动能定理即可求出物块与薄板碰撞前的速度；在碰撞过程中满足动量守恒，再结合能量守恒即可求出弹簧被压缩到位置B时的弹性势能。
（1）物块落到薄板上的速度为v0，根据动能定理可得：
解得：
（2）在B位置与薄板碰撞满足动量守恒：
在位置B处的弹性势能为EP，系统从位置B开始压缩后返回位置O
根据能量守恒可得：
联立解得：
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
