题目内容
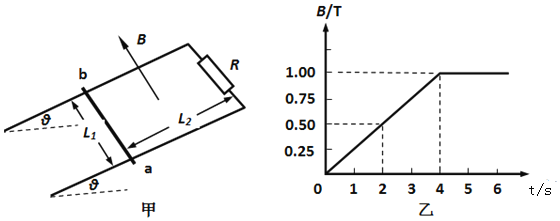
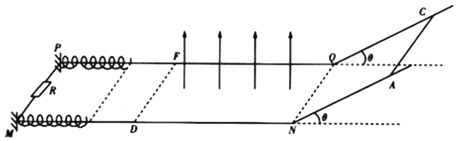
【题目】如图所示，水平面上有两条相互平行的光滑金属导轨PQ和MN间距为d，左侧P与M之间通过一电阻R连接，两条倾角为θ的光滑导轨与水平导轨在N、Q处平滑连接，水平导轨的FDNQ区域有竖直方向的匀强磁场，磁感应强度为B，磁场区域长度为x。P，M两处有套在导轨上的两根完全相同的绝缘轻质弹簧，其原长为PF，现用某约束装量将两弹簧压缩到图中虚线处，只要有微小扰动，约束装置就解除压缩。长度为d，质量为m，电阻为R的导体棒，从AC处由静止释放，出磁场区域后向左运动触发弹簧。由于弹簧的作用，导体棒向右运动，当导体棒进入磁场后，约束装置重新起作用，将弹簧压缩到原位置.
（1）若导体棒从高水平导轨高h的位置释放，经过一段时间后重新滑上斜面，恰好能返回原来的位置，求导体棒第一次出磁场时的速率
（2）在（1）条件下，求每根弹簧被约束装置压缩后所具有的弹性势能。
（3）要使导体棒最终能在水平导轨与倾斜导轨间来回运动，则导体神初始高度H及每根弹簧储存的弹性势能需要满足什么条件？
【答案】(1)v2=
-
(2) Ep=
(3) H＞
且EP≥
【解析】
（1）导体棒在倾斜轨道上向下滑动的过程中，根据机械能守恒定律有：
mgh=
解得：v1=
导体棒越过磁场的过程中，根据动量定理可得：
-BdIt=mv2-mv1，
根据电荷量的计算公式q=It=
=
解得v2=-；
（2）设解除弹簧约束，弹簧恢复压缩后导体棒的速度为v3，根据导体棒与弹簧组成的系统机械能守恒可得：
=
+2Ep；
导体棒向右通过磁场的过程中，同理可得：
v4=v3-；
由于导体棒恰好能回到原处，所以有v4=v1，
联立解得：Ep=；
（3）导体棒穿过磁场才能把弹簧压缩，故需要满足v2＞0，
即H＞
要使导体棒不断地运动下去，导体棒必须要回到NQ位置，则：
EP=
≥
要使导体棒最终能在水平导轨与倾斜导轨间来回运动，H＞，且弹簧的弹性势能满足EP≥。
