题目内容
3.一对反粒子是指质量相同、电量相等电性完全相反的粒子,如电子(${\;}_{-1}^{0}$e)和正电子(${\;}_{1}^{0}$e)就是一对反粒子;当静止的质子和反质子质相遇时可发生湮灭,并发出两个波长相同的光子,已知质子质量为m,光速为c,普朗克常量h,则发出的光子的波长为$\frac{h}{mc}$;上述过程能否发出两个波长不相同的光子?理由是不能,否则总动量不为零,违背动量守恒定律.分析 根据爱因斯坦质能方程和能量子公式E=hγ列式求解发出的光子的波长;结合动量守恒定律分析两个光子的质量关系.
解答 解:静止的质子和反质子质相遇时可发生湮灭,并发出两个波长相同的光子,根据爱因斯坦质能方程和能量子公式,有:
2mc2=2E
E=hγ=$\frac{hc}{λ}$
联立解得:
λ=$\frac{h}{mc}$
上述过程系统初动量为零,故末动量也为零,故两个光子的动量应该大小相等,方向相反,速度相等,根据λ=$\frac{h}{P}$,波长相等;
故答案为:$\frac{h}{mc}$;不能,否则总动量不为零,违背动量守恒定律;
点评 本题综合考查了爱因斯坦质能方程、爱因斯坦的光子说、光的波粒二象性,关键是根据规律列式分析,不难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一平行板电容器,两板之间距离d与正对面积S都可以在一定范围内调节,电容器两板与电池两极始终保持相连接,以C表示电容器的电容,以Q表示电容器的电量,以E表示两极板间的电场强度,则( )
| A. | 当d增大、S不变时,C减小,E减小 | B. | 当S增大、d不变时,C增大,E增大 | ||
| C. | 当d减小,S增大时,C增大、Q增大 | D. | 当S减小、d减小时,C不变、Q减小 |
14. 伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次.假设某次实验伽利略是这样做的:在斜面上任取三个位置A、B、C.让小球分别由A、B、C滚下,如图所示,A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,小球由A、B、C运动到斜面底端时的速度分别为v1,v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是( )
伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次.假设某次实验伽利略是这样做的:在斜面上任取三个位置A、B、C.让小球分别由A、B、C滚下,如图所示,A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,小球由A、B、C运动到斜面底端时的速度分别为v1,v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是( )
 伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次.假设某次实验伽利略是这样做的:在斜面上任取三个位置A、B、C.让小球分别由A、B、C滚下,如图所示,A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,小球由A、B、C运动到斜面底端时的速度分别为v1,v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是( )
伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次.假设某次实验伽利略是这样做的:在斜面上任取三个位置A、B、C.让小球分别由A、B、C滚下,如图所示,A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3,小球由A、B、C运动到斜面底端时的速度分别为v1,v2、v3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下运动是匀变速直线运动的是( )| A. | $\frac{{s}_{1}}{{t}_{1}^{2}}$=$\frac{{s}_{2}}{{t}_{2}^{2}}$=$\frac{{s}_{3}}{{t}_{3}^{2}}$ | B. | $\frac{{v}_{1}}{2}$=$\frac{{v}_{2}}{2}$=$\frac{{v}_{3}}{2}$ | ||
| C. | $\frac{{v}_{1}}{{t}_{1}}$=$\frac{{v}_{2}}{{t}_{2}}$=$\frac{{v}_{3}}{{t}_{3}}$ | D. | s1-s2=s2-s1 |
8.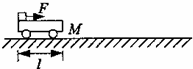 如图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车最右端时,小车运动的距离为s.在这个过程中,下列说法正确的是( )
如图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车最右端时,小车运动的距离为s.在这个过程中,下列说法正确的是( )
 如图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车最右端时,小车运动的距离为s.在这个过程中,下列说法正确的是( )
如图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车最右端时,小车运动的距离为s.在这个过程中,下列说法正确的是( )| A. | 物块到达小车最右端时具有的动能为F(l+s) | |
| B. | 物块到达小车最右端时,小车具有的动能为fs | |
| C. | 物块克服摩擦力所做的功为f(l+s) | |
| D. | 物块和小车增加的机械能为fs |
13. 如图所示,理想变压器的原、副线圈匝数比n1:n2=1:10,副线圈与阻值R=20Ω的电阻相连,原线圈两端所加的电压u=20$\sqrt{2}$sin20πt(V),则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=1:10,副线圈与阻值R=20Ω的电阻相连,原线圈两端所加的电压u=20$\sqrt{2}$sin20πt(V),则( )
 如图所示,理想变压器的原、副线圈匝数比n1:n2=1:10,副线圈与阻值R=20Ω的电阻相连,原线圈两端所加的电压u=20$\sqrt{2}$sin20πt(V),则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=1:10,副线圈与阻值R=20Ω的电阻相连,原线圈两端所加的电压u=20$\sqrt{2}$sin20πt(V),则( )| A. | 交流电压表的示数为20$\sqrt{2}$V | B. | 副线圈输出交流电的频率为50Hz | ||
| C. | 电阻R上消耗的电功率为2kW | D. | 副线圈中电流的最大值为1 A |

 如图所示,间距为L的平行光滑金属导轨与水平面的夹角为θ,导轨电阻不计.导体棒ab、cd垂直导轨放置,棒长均为L,电阻均为R,且与导轨电接触良好.ab棒处于垂直导轨平面向上、磁感应强度B1随时间均匀增加的匀强磁场中.Cd棒质量为m,处于垂直导轨平面向上、磁感应强度恒为B2的匀强磁场中,恰好保持静止.ab棒在外力作用下也保持静止,重力加速度为g.
如图所示,间距为L的平行光滑金属导轨与水平面的夹角为θ,导轨电阻不计.导体棒ab、cd垂直导轨放置,棒长均为L,电阻均为R,且与导轨电接触良好.ab棒处于垂直导轨平面向上、磁感应强度B1随时间均匀增加的匀强磁场中.Cd棒质量为m,处于垂直导轨平面向上、磁感应强度恒为B2的匀强磁场中,恰好保持静止.ab棒在外力作用下也保持静止,重力加速度为g.